|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 111 a 115 |
| Solución
111: La hora publicitaria. Por: Josep María Albaigès |
|
|
Si llamamos x al ángulo que el
horario forma con la línea de las 10 h, el que el minutero
formara con las 12 h será 12x, pues el minutero avanza 12
veces más aprisa que el horario. Siendo el ángulo
entre las 10 y las 12 de 60º, la ecuación es obvia:
12x = 60 - x De donde resulta x = 60/13 de grado. Puesto que 360º corresponden a 12 h, el ángulo equivale a 2/13 de hora. Es decir, que la hora marcada por el reloj es 10h 9m 13s 11/13. Problema número 2. Si el ángulo entre el horario y el minutero fuera exactamente de 120º, por consideraciones similares obtenemos que el ángulo x vale en este caso 60/11 de grado, es decir, que el reloj marcaría las 10h 10m 54s 6/11. Pero entonces el segundero marcaría unos 54 s, muy lejos de los 30s. Se concluye que el punto óptimo que buscamos ha tenido lugar hace aproximadamente medio minuto. Supongamos ahora que el ángulo del horario con las 10h es x - e . Recordando que el segundero va 60 veces más aprisa que el minutero, los valores quedan ahora convertidos en:
En primera aproximación, podemos concluir que e deberá ser del orden de medio minuto horario (o sea unos 3º). Veamos los ángulos entre las respectivas manecillas.
Unos tanteos rápidos concluyen que el mínimo se alcanza cuando el tercer paréntesis se anula, o sea para e = 1560/7909 grados. Con lo cual el ángulo buscado vale: x = 41580/7909 grados. Este ángulo equivale a 1386/7909 de hora. O sea que son las: 10h 10m 30s 630/719 Como se ve, el resultado es de lo mas preciso. Los ángulos valen: a 2 = 122,17º a 3 = 120,00o |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
(obvio)
| Solución
112: El monje budista viajero. Por: Javier García Algarra |
|
La figura representa la distancia a la
que se encuentra el monje de la base de la montaña en función
del tiempo. 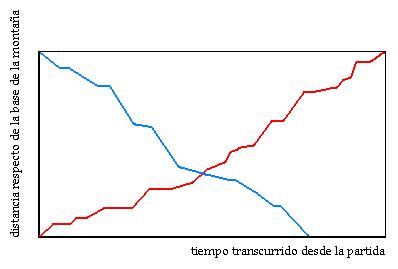 El camino
de ida se ha representado en rojo y el de vuelta en azul. Como el
enunciado dice que en el camino de regreso el monje tiene una mayor
velocidad, en valor medio, el tiempo transcurrido en recorrer la
distancia es menor. Es obvio que las dos líneas se cruzarán
en un punto, da igual el trazado que hagamos, y en ese instante
del día es cuando el monje pasa por el mismo sitio tanto
en el ascenso como en el descenso. Daría igual que la velocidad
media del descenso fuese menor que la del ascenso, en ese caso la
línea azul cortaría el eje horizontal de la gráfica
más hacia la derecha pero también tendría un
punto de intersección con la línea roja.
|
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
113: El número perdido. Por: Anónimo. |
|
| El número que falta es el 6, de este modo la suma de todos los cuadrados de cuatro números es 20. | |
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
114: Criptoadivinanza. Por: Anónimo. |
|
| Las tres letras de cada una de las igualdades son las primeras del nombre de una piedra preciosa y la de la derecha la inicial del color correspondiente. Así AMAtista = Púrpura, RUBí = Rojo, ZAFiro = Azul y ESMeralda = Verde. | |
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
115: Los vasos usados. Por: Anónimo |
|
| El número de vasos que pueden reciclarse es 63. Con los 505 vasos iniciales se fabrican 56 reciclados ( y sobra 1 ), con esos 56 pueden fabricarse otros 6 ( y sobran 2), y con esos 6 finales más los tres que han sobrado, uno más. Total : 63. | |
| Ver Enunciado de este problema | |
|
||||||
