JUEGOS DE INGENIO DEL CLUB MENSA
(ENUNCIADOS 081 a 085) |
|
|
| Enunciado 081: Dominó alfanumérico
|
|
Hallar el valor de la
cifra que falta.

|
| Autor: |
Abby Salny, psicóloga supervisora de Mensa. |
| Publicado en: |
OMNIA-23. Mayo de 1990 |
| Dificultad: |
* |
| Solución: |
Pulse aquí |
 |
|
|
| Enunciado 082: Dos sucesiones numéricas casi iguales.
|
|
Primer enunciado:
¡Encuentra
el cuarto término de la sucesión que empieza 1, 2, 3!
Segundo enunciado:
Encuentra el cuarto
término de la sucesión que empieza 1, 2, 3!
|
| Autor: |
Ricardo C. Burrows. |
| Publicado en: |
CARROLLIA-36 , Marzo de 1993 |
| Dificultad: |
** |
| Solución: |
Pulse aquí |
 |
|
|
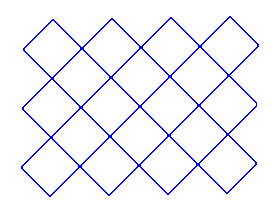
| Enunciado 083: Malla romboidal.
|
|
Colocar los números:
1,
6, 8, 9, 11, 12, 15, 16, 18, 19, 21, 22, 25, 26, 30, 31, 36,
37, 40, 41, 42, 45, 46, 47, 48, 49, 50, 51, 56, 57 y 61.
En los nudos de la malla
romboidal siguiente de modo que, la suma de los cuatro números
que estén en los vértices de cualquiera de los
dieciocho rombos sea igual a 124.
|
| Autor: |
Antonio Cebrián. |
| Publicado en: |
CARROLLIA-54. Septiembre de 1997 |
| Dificultad: |
** |
| Solución: |
Pulse aquí |
 |
|
|
| Enunciado 084: Otra ecuación de Cebrián. |
|
Calcular el mayor valor
entero que puede tomar x
para que la siguiente fracción sea un número entero:
y = (x3 + 4x2
+ 212 x + 3132)/(x2 + 5x +216)
|
| Autor: |
Antonio Cebrián. |
| Publicado
en: |
International Mensa Journal . Octubre de 1997 |
| Dificultad: |
*** |
| Solución: |
Pulse aquí |
 |
|
|
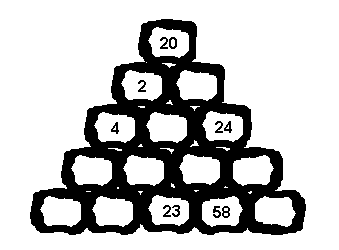
| Enunciado 085: El montón de piedras. |
Cada una de las piedras
del montón reposa sobre dos de la fila inferior. El número
de cada piedra representa la diferencia entre los números de las
piedras sobre las que se sustenta. Completar los números que faltan,
sabiendo que en la fila inferior los dígitos del 0 al 9 sólo
aparecen una vez en el conjunto de todos los números.
|
| Autor: |
Therese Moodie-Bloom |
| Publicado en: |
International Mensa Journal . Octubre de 1997 |
| Dificultad: |
* |
| Solución: |
Pulse aquí |
 |
|
|