|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 176 a 180 |
| Solución
176: Una variante de Tartaglia. Por: Josep María Albaigès |
|
|
Acometamos el problema de forma analítica.
Llamaremos: a,b,c: Lados del triángulo ha: Altura correspondiente al lado a. ma: Mediana correspondiente al lado a. ua: Proyección de ma sobre a. 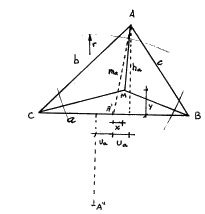 Situado el triángulo
de la forma habitual y tomando como origen de coordenadas A’, centro
del lado a, tomando v. gr. MA como la hipotenusa del triángulo
a construir, es inmediato que deberá Situado el triángulo
de la forma habitual y tomando como origen de coordenadas A’, centro
del lado a, tomando v. gr. MA como la hipotenusa del triángulo
a construir, es inmediato que deberá cumplirse MB2+ MC2= MA2. Expresando cada segmento según Pitágoras se tendrá: 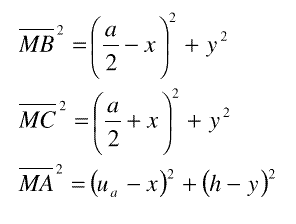 Sumando y simplificando, pronto se llega a: 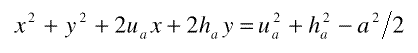 Igualdad que podemos escribir: 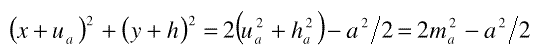 ¡Sorpresa! El lugar geométrico buscado resulta ser un arco de circunferencia con centrosituado en el punto A”, antisimétrico de A respecto a A’, y radio 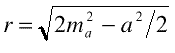 Por
cierto que este valor es fácilmente calculable. En geometría
métrica elemental se demuestra que Por
cierto que este valor es fácilmente calculable. En geometría
métrica elemental se demuestra que y sustituyendo, se obtiene: Si, como es costumbre, se hace p = (a+b+c)/2, se halla finalmente: 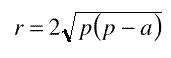 Como el anterior razonamiento hubiéramos podido hacerlo también tomando OB y OC como hipotenusa, se obtendrán en general tres arcos de circunferencia, que configuran la solución. Algunos de ellos pueden quedar fuera del triángulo, lo que los invalidará. Como ejercicio, se propone dibujar la curiosa figura que resulta cuando el triángulo es equilátero. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
177: El condenado. Por: Varios |
|
|
Solución de J. Beleta: Si dices verdad a la hoguera y si mentira veneno. Solo puedes pensar en una frase que sea mentira si te queman o en una frase que sea verdad si te envenenan. Las frases posible, son casi evidentes: "no moriré en la hoguera" o "moriré envenenado". Solución de El Mendigo: A mi se me ocurre que otra posibilidad es decir una frase que no sea ni verdad ni mentira, o, en su defecto, que el interlocutor no lo pueda saber o demostrar. Por ejemplo: a) Dentro de 215 años hará frío en Albacete. - no demostrable por razón de tiempo y, como mínimo, durante 215 años. b) El número de pelos que tengo en el cuerpo oscila entre los 2 y los 7.000.000. - esta frase está más cogida por los pelos ya que podrían quemar al explorador y depilarle completamente. c) Si estás siempre saltando alguna vez saldrás volando. - sólamente demostrable una vez completada la clausula "siempre". d) Si me matais con veneno os caerá un aerolito en la cabeza. - seguramente con esta frase el indígena se volvería loco ("si le quemamos no sabremos si decía la verdad y si le envenenamos no sabemos si nos mintió así que le envenenamos, nos vamos al espacio, y nos tiramos un aerolito a la cabeza y ..."). |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
178: Los maridos engañados. Por: Varios. |
|
|
Solución de J. Beleta: Para mi lo mas simple es ponerte en el pellejo de uno de los maridos y reproducir su manera de pensar. Así mismo es útil suponer que SOLO hay una infidelidad, para resolver primero el caso sencillo. En este caso sencillo, si te dicen que hay una infidelidad y tu no la conoces, de acuerdo al enunciado del problema, es tu esposa, por lo que lo sabes de forma inmediata y la expulsas a la mañana siguiente y si la conoces, alguien hará el razonamiento anterior y expulsará a la suya a la mañana siguiente. Si a la mañana siguiente nadie expulsa a su mujer será porque los demás deben saber que hay dos infidelidades y tu deduces que la segunda es la de tu mujer, ya que solo conoces una. Llegado a este punto, por simple inducción se deduce que si tu conoces n infidelidades y el día n no se expulsan n mujeres, hay una infidelidad mas que es la tuya y el dia n+1 se expulsarán n+1 mujeres. De esta forma, queda claro que hasta el dia 40, los 40 cortesanos, que cada uno conocía las 39 infidelidades de los otros, no supieron que sus respectivas esposas tambien les eran infieles y todos las expulsan el día 40. Solución de El Mendigo: La explicación Beletiana traía como consecuencia que el primer día el cortesano evaluase la posibilidad de que hubiese una sola infidelidad, el segundo dos infidelidades y así sucesivamente. Señores, ¿cómo encajar esta propuesta en un entorno donde todos saben que hay 39 esposas infieles como mínimo?. ¿Realmente cabe pensar que el cortesano evalúa el primer día la existencia de 1 infidelidad o no?, si realmente no se evalúa el primer día la existencia de 1 infidelidad entonces ¿qué demonios se evalúa el primer día?. Tenía lasensación de que el tiro, (desarrollo matemático), había dado en el blanco pero que no se había explicado correctamente como hacer para apuntar la flecha, (desarrollo lógico según esta metáfora). ¿Alguien se atrevería a retomar la solución aportada por el maestro? Iniciaba pues mi razonamiento ¿divergente? reconociendo dos puntos claros en el modelo de JB que si se acomodaban a mi pensamiento. Uno es la capacidad, necesidad, de pensar sobre el pensamiento del otro. El otro punto es el devenir de los días para la reducción de posibilidades. En este sentido me pareció conveniente provocar ciertas relaciones en el modelo teórico. Por ejemplo: a) se supone que cuando dos cortesanos departen sobre las infidelidades del reino hablan de que existen 38 infidelidades. (Lógico, pues pueden hablar de las infidelidades de los demás, no de la suya, que la desconocen, ni la de su interlocutor, para que se siga manteniendo en el anonimato). b) En cuanto se une un tercer interlocutor a la conversación se hablará de que existen 37 infidelidades. (Apliquen el mismo razonamiento deductivo que antes) c) En cuanto se una un cuarto interlocutor a la conversación se hablaría de que existen un máximo de 36 infidelidades. Y así sucesivamente. Obsérvese que en estas relaciones da igual quienes sean los cortesanos. Solamente hace falta saber el número de ellos que departen en la conversación para reducir el ordinal de esposas infieles reconocidas por el oratorio. A efectos expositivos, y de simplificación del modelo a elaborar, propongo que trabajemos con cinco cortesanos. Parece claro pensar que las propiedades expuestas para cinco elementos serán fácilmente extrapolables a las cuarenta unidades que aquí se debaten. A mis cinco cortesanos los llamaremos C1, C2, C3, C4 y C5. Es importante que también tengan en cuenta que el modelo tiene que solucionarse a los cinco días de su puesta en marcha. Pensemos ahora. ¿Qué es lo que cruza por la mente de uno de los cortesanos?. Empecemos. a) Si C1 habla con C2 ambos reconocerán que existen 3 infidelidades (obvio: C3, C4, y C5). b) Se incorpora C3 a la conversación. Se hablará sólo de 2 infidelidades (C4 y C5). c) Se incorpora C4 a la conversación. Se hablará de que sólo existe 1 infidelidad (C5). Que deriva de cada uno de estos puntos para nuestro primer interlocultor, C1. a) En este punto C1 debe pensar que C2 piensa que hay 3 infidelidades. La refutación de este pensamiento sólo puede traer dos consecuencias: que C2 conozca la existencia de una infidelidad más o que C2 entienda que es objeto de infidelidad. b) En este punto C1 debe pensar que C2 debe pensar que C3 debe pensar que existen 2 infidelidades. (A propósito no incorporamos ahora lo que C1 tiene sobre el pensamiento de C3). Insistamos, pues, en la relación de C1 sobre C2 sobre C3. ¿Empiezan a entrever la relación de pensamiento que elabora C1? ¿y lo qué obtendremos?. La refutación de este pensamiento sólo puede traer dos consecuencias para C1-C2: que C3 conozca la existencia de alguna infidelidad más o que C3 entienda que es objeto de infidelidad. La información aquí obtenida, su demostración de falsedad, se incorporará con naturalidad a la evaluación de la primera proposición a) pensamiento C1-C2. c) En este punto C1 pensará que C2 piensa que C3 piensa que C4 piensa que existe una sola infidelidad: la del infortunado C5. La reacción en cadena es evidente; en la línea de pensamiento C1-C2-C3 se empieza a cuestionar el número de infidelidades. Este desarrollo lo podemos hacer permutando todos los elementos sobre C1. Gráficamente podría quedar de la siguiente manera: 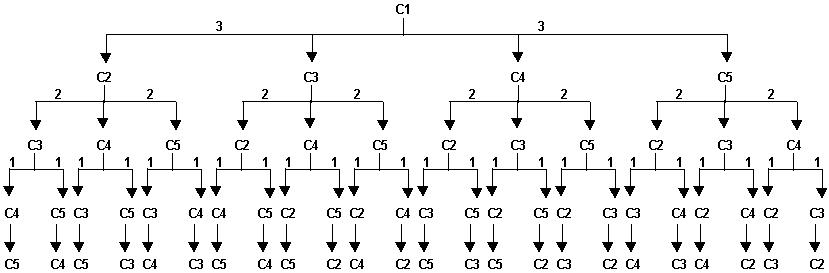 El ejemplo que hemos desarrollado equivaldría a la primera rama del árbol (primera de la izquierda). En las flechas se incorporan el número de infidelidades que se considera en la conversación del grupo. (pe, C1-C2. 3, C1-C2-C3-C4, 1).Es de suponer que el árbol presenta todas las relaciones causales posibles. Obsérvese los cinco niveles que equivaldrán a los cinco días de decisión. ¿Cómo trabaja el pensamiento de C1 en este árbol de combinaciones?. Desglosémoslo trabajando sobre la primera rama de la izquierda. El primer día no expulsan al cónyuge C5 (realmente no expulsan a nadie). ¿Qué ha pasado con la cadena de pensamientos?. C1 ya no puede pensar que C2 debe pensar que C3 debe pensar que C4 debe pensar que C5 tiene una mujer infiel. Obviamente esta línea de pensamiento, tan larga, queda abandonada. Con igual razonamiento podemos eliminar todas las líneas combinatorias de pensamiento de la última fila. Para C1 es claro que estas líneas de pensamiento han quedado claramente refutadas en este día. El pensamiento de C1 no debe derivar, por tanto, en si se evaluaba la existencia de 1 infidelidad sino en refutar taxativamente estas líneas de razonamiento en este día. ¿Qué ocurre el segundo día?. Evaluamos el pensamiento C1-C2-C3. El razonamiento C1-C2-C3-C4 se ha descubierto falso el día antes como se preveía (de igual manera el pensamiento C1-C2-C3-C5). En este día, C4 obviamente no ha expulsado a su cónyuge y tampoco C5. Urge pensar que el pensamiento C1-C2-C3 queda al descubierto como falso. El pensamiento C1-C2 se prepara para ser evaluado al día siguiente. Obsérvese que todo la estructura deductiva ronda en la cabeza de C1. En este modelo resulta indiferente lo que realmente piensen el resto de los cortesanos sino lo que efectivamente construye C1 en su razonamiento. ¿Qué ocurren los días tercero y cuarto? Aplicando el mismo desarrollo inductivo es fácil sostener como las proposiciones se demuestran negativas y como se va incorporando la información cada día que pasa. Lógicamente al argumentar razonadamente que C2, o C3 o C4 o C5, no reaccionan el cuarto día le permite deducir a C1 que su esposa es infiel. Este es el único nivel en que C1 incorpora información no conocida a su sistema de deducción. Volviendo a nuestro modelo de 40 cortesanos, a priori C1 sabe que el modelo se tiene que resolver en el día 39. Resulta obvio que si, por ejemplo, C4 aparece en un primer nivel de pensamiento, C1-C4-38 infidelidades, es de esperar que el resto de posiciones que ocupa C4 en ramas más bajas tienen que dar necesariamente un resultado negativo. Supongo que a C1 le resulta la espera más tranquila pudiendo tachar, de su estructura de pensamiento, que líneas van resultando imposibles cada día que pasa, aunque tampoco le tendrá que importar mucho si se va 39 días de vacaciones con la seguridad de que cuando vuelva estará a punto de resolverse el acertijo, ya que a priori conoce la información que se incorporará cada día. Y ahora, amable y paciente lector, en mi opinión el modelo así expuesto permite, obliga, a eliminar posibilidades; cada día incorpora nuevos valores a la información. Sólo cada día que pasa permite aflorar que los diferentes razonamientos C1-C2-C3-C4-C5... son falsos. No se trata pues de que se evalúe la posibilidad de que haya, en un momento dado, 10 cónyuges infieles (cuestión que a mi juicio no parece aplicable) sino de que se han establecido y refutado ciertas líneas de pensamiento imposibles. El cortesano C1 se queda más tranquilo eliminando posibilidades y yo también. La exposición del modelo del maestro me dejaba un vacío bastante angustioso durante 39 días. Había dado en el blanco pero nos había ocultado como había apuntado la flecha, ¿lo habría hecho a propósito?, ¿realmente basta con refutar cada día la no-existencia de un número equivalente de infidelidades? En fin. Amable y paciente lector lo dejo a tu juicio. Largo y, probablemente, tedioso, pero si no lo cuento reviento. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
179: Serie de vocales. Por: Philip Carter. |
|
| La serie se construye con las vocales del nombre de los planetas en orden de cercanía al Sol, por lo que faltan la de Plutón, luego la solución es UO. | |
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
180: ¿Qué hay en común? Por: Anónimo. |
|
| Las cuatro palabras son anagramas de nombres de río: TÁMESIS, EBRO, NILO, SEGURA. | |
| Ver Enunciado de este problema | |
|
||||||