JUEGOS DE INGENIO DEL CLUB MENSA
(ENUNCIADOS 001 a 005)
 
Cada enunciado viene acompañado de su correspondiente resolución. Se aconseja evitar consultar ésta de buenas a primeras pues, de obrar así, lo que se ejercita es el botón del ratón y no la mente. El número de estrellas indica la dificultad del problema.
 
Problema 001 Dos números consecutivos en la Lotería Primitiva **
Problema 002 Un criptograma sencillo *
Problema 003 Las obras desvían la gravedad ***
Problema 004 Una ecuación curiosa. ***
Problema 005 La telaraña pentagonal *
Enunciado 001: Dos números consecutivos en la Lotería Primitiva
Determinar la probabilidad de que en un sorteo de Lotería Primitiva aparezcan al menos dos números consecutivos cualesquiera.
Autor: Andrés García Parrilla.
Publicado en: OMNIA-32. Febrero de 1992
Dificultad: **
Solución: Pulse aquí
Enunciado 002: Un criptograma sencillo
Resuelva el amable lector el siguiente criptograma. Cada ? representa un símbolo que debe encontrarse.
 
M I L
+ M I L
_ _ _ _ _ _ _ _
? ? ? ? ? ? ? ?
Autor: No especificado.
Publicado en: CARROLLIA-31. Febrero de 1991
Dificultad: *
Solución: Pulse aquí
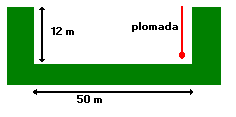
Enunciado 003: Las obras desvían la gravedad
Mi empresa ejecuta una obra, de la que se ha completado la excavación. Esta consiste, aproximadamente, en un vaciado de planta cuadrada, con 50 m de lado y 12 m de profundidad. Conversando un día con un arquitecto compañero, se nos ocurrió si la plomada librada a lo largo de uno de los lados de la excavación se desviaría mucho de la vertical como consecuencia del vaciado.

¿Puede calcularlo el amable lector?. Tome la densidad del terreno igual a 2000 kg/m³ y recuerde que el radio de la tierra es 6730 km, y su masa, 6*1024 kg.
 
 


Autor: Josep María Albaigès.
Publicado en: CARROLLIA-31. Febrero de 1991
Dificultad: ***
Solución: Pulse aquí
Enunciado 004: Una ecuación curiosa.
Probar que la siguiente ecuación, no tiene más soluciones enteras que (1,0) y (2,1). 
            
2x  - 3y  = 1
Autor: Miguel Angel Lerma.
Publicado en: CARROLLIA-50. Septiembre de 1996
Dificultad: ***
Solución: Pulse aquí
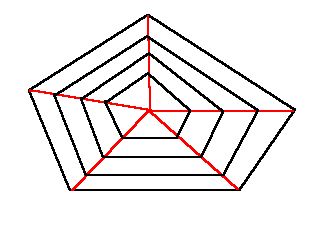
Enunciado 005: La telaraña pentagonal
Colocar los números impares del 1 al 31, ambos inclusive, y los números 20,32,34,38 y 40 en los 20 vértices de los 4 pentágonos y en el centro de la tela de araña, de manera que la suma de los 5 números de los vértices de cualquier pentágono sea igual a la suma de los cinco números de cualquier radio e igual a 100.

Autor: A. Cebrián
Publicado en: CARROLLIA-36. Febrero de 1993
Dificultad: *
Solución: Pulse aquí
(c) JGA, 1996 Los contenidos son de los autores, Mensa no sostiene ninguna idea Página principal