JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 001 a 005
Solución 001: Dos números consecutivos en la Lotería Primitiva
Por: Miguel Angel Lerma
La solución más sencilla pasa por calcular el número de combinaciones en las que no hay números consecutivos y restarlo luego del total.

Consideremos los dos conjuntos siguientes:

C1 = Combinaciones de 6 números del 1 al 49 tales que entre ellos no hay dos consecutivos.

C2 = Combinaciones cualesquiera de números del 1 al 44.

Ambos conjuntos tienen igual número de elementos, dado que existe entre ellos la siguiente correspondencia biunívoca: (a,b,c,d,e,f) <-> (a,b-1,c-2,d-3,e-4,f-5)

dónde a,b,c,d,e,f son números entre 1 y 49 tales que no hay entre ellos dos consecutivos. Por ejemplo, la combinación (1,5,7,20,35,49) de C1 se correspondería con la (1,4,5,17,31,44) de C2. El número de C2 es el combinacional de 44 sobre 6 = 7.059.052. Puesto que C1 y C2 tienen el mismo número de elementos Card(C1)=Card(C2)=7.059.052.

La cantidad total de combinaciones de la Lotería Primitiva es el combinacional de 49 sobre 6 = 13.983.816.

Luego, el número de tales combinaciones en las que no hay dos elementos consecutivos es la diferencia: 13.983.816 - 7.059.052 = 6.924.764

La probabilidad de que salgan dos números consecutivos cualesquiera en un sorteo es, en consecuencia 49,52%.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 002: Un criptograma sencillo
Por: No especificado
Los símbolos son: M M X C V I I I .

La suma está expresada en numeración romana. Así:

          M I L                     1 0 4 9
+         M I L               + 1 0 4 9
_ _ _ _ _ _ _ _                 _ _ _ _ _
M M X C V I I I                 2 0 9 8


Entre los bloqueos conceptuales se encuentra el de falso hecho admitido, por ello para la resolución de problemas no hay nunca que dar por sentado más que lo que específicamente se exprese en el enunciado. En este caso, admitir sin más, que los símbolos expresan dígitos, cierra el camino hacia la solución.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 003: Las obras desvían la gravedad
Por: Josep María Albaigès.
La aceleración de la gravedad g vale 9,81 m/s². 
g = GM/R² = 9.81 m/s²
siendo G la constante de gravitación universal, M la masa de la Tierra y R su radio.

El peso de un cuerpo en la superficie terrestre es la composición de las atracciones sobre él de todos los átomos de la Tierra, y equivale a la que ejercería la masa de ésta concentrada en su centro. El hueco de la excavación supone introducir en ese conjunto una asimetría substractiva, cuyo resultado neto es lógicamente una repulsión del mismo valor que la atracción gravitatoria que ejercería el volumen de tierras del hueco.

Se puede asimilar también ésta, bastante aproximadamente, a la que ejercería una masa equivalente contentrada en el centro de gravedad de la excavación, o sea: 
g' = Gm'/r'²
Donde las respectivas masa y distancia de acción valen: 
m' = 50.50.12.2000 = 6.107 kg
r' = (25² + 6²)½  = 25,71 m
El cociente entre ambas fuerzas vale: 
g'  6.107.(6,37.106)²
- = -------------------
g   6.1024.(25,71)²

g'/g = 6,14*10-7
La componente horizontal de esa fuerza vale:
 g'x /g  = 6,14.10-7 (25/25,71) = 5,97 .10-7
Este es el ángulo que se desviará la plomada de la vertical. En una distancia de 12 metros, equivale a: 
x = 12.5,97.10-7 m = 7,16.10-6 m = 0,00716 mm
Esta desviación es ciertamente inapreciable, pero no lo sería tanto en el caso de una gran excavación, como las de algunas explotacoines metalúrgicas a cielo abierto en Chile o Sudáfrica, en que algunas de las dimensiones anteriores pueden ser de kilómetros. Para un hueco de 500*500*120 m, la desviación de la plomada en el fondo sería de ¡0,7 mm!, claramente perceptible.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 004: Una ecuación curiosa.
Por: A. Cebrián.
Puesto que la diferencia es positiva se cumple que x > y. Procediendo al cambio de variable x = a+y la expresión queda: 
        
       2a+y  - 3y = 1 =>  2a 2y - 3y = 1 => 2a(10/5)y - 3y = 1

          
       => 2 a 10 y = 15 y + 5 y     (I)


El primer miembro de (I) termina en "y" ceros. Vamos a ver en cuantos ceros termina el segundo miembro. Obtenemos las primeras potencias de 15 y 5.

y 15y 5y La suma 15y + 5y termina en "y" ceros
0 1 1 0
1 5 5 1
2 225 25 1
3 3375 125 2
4 50625 625 1
5 759375 3125 2


Si nos fijamos en las terminaciones vemos que:

Cuando y>2 15y termina 5y termina La suma termina
Impar 375 125 500 (2 ceros)
Par 625 625 350 (1 cero) 
 Es así porque 375 x 15 termina en 625 y 125 x 5 termina en 625
 minetras que 625 x 15 termina en 375 y 625 x 5 en 125
Luego la igualdad (I) no se cumple para y>2: Primer miembro 2 ceros, segundo miembro 1 cero (225+25=250).

Como consecuencia, la ecuación planteada sólo puede cumplirse para y<=2, concretamente para (1,0) y (2,1).
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 005: La telaraña pentagonal
Por: A. Cebrián

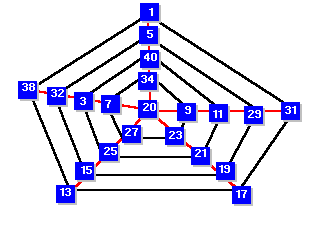Ver Enunciado de este problema
(c) JGA, 1996 Los contenidos son de los autores, Mensa no sostiene ninguna idea Página principal