JUEGOS DE INGENIO DEL CLUB MENSA
(ENUNCIADOS 041 a 045) |
|
|
| Enunciado 041: Trasvases, un problema antiquísimo.
|
El bachiller Juan Pérez de
Moya, profesor de matemáticas en la Universidad
de Salamanca, publicó en el año 1562 su ARITHMETICA
PRACTICA Y SPECULATIVA, libro de tanto éxito que
siguió editándose a la largo de los siglos, hasta
tiempos de Carlos III. El libro nono y último de
este tratado se presenta en forma de diálogo entre dos
estudiantes que debaten temas sobre artimética, Sofronio
(¿lo llama así porque tiene que sufrir a Antímaco?),
defiende la utilidad de esta ciencia, sin embrago, Antímaco
dice no tener necesidad de ella, y tiene por opinión
que "no hay ninguno que sepa contar, teniendo buenos dineros".
En la segunda parte del diálogo se juntan otros dos estudiantes,
Damón y Lucilio y "se prosigue la plática
entre todos cuatro, diciendo cada uno las preguntas o dislates
que sabe, todo por términos comunes de aritmética".
Este libro nono ha sido reeditado por la Universidad
de Zaragoza con prólogo y notas de R. Rodríguez
Vidal , catedrático que fue de Anáilisis
matemático y Algebra de dicha universidad.¿Por qué
sólo el libro nono?. Seguramente porque, como afirma el
autor "... puede leerse con independencia de los otros y constituye
la primera colección de Matemática Recreativa, o
amenidades matemáticas que se publica en castellano". Lo
estudiantes de nuestro diálogo acuerdan plantear, por turno,
una cuestión y llegado el de Damón dice:
Ahora señores,
conformes al al concierto, quiero decir como dos caminantes llevaban ocho
arrobas de vino, y en el camino determinaron de deshacer la compañía
y de apartarse cada uno por su cabo: y habiendo de partir por la mitad
el vino hallaron que no tenían sino dos medidas. La una cabía
tres arrobas y la otra cinco: pídese, ¿cómo partirán
con estas dos medidas diferentes el vino, para que cada uno lleve cuatro
arrobas que le vienen de su parte?
Damón explica
en seguida los trasvases necesarios para conseguir el propósito
y termina diciendo:
..y como dije ocho,
pude decir diez arrobas, y las medidas sean una de tres y otra de siete.
Aquí Rodríguez Vidal hace el siguiente comentario:
Al lector que acepte
la invitación del texto para hacer el trasvase con vasijas de 10,
7 y 3 medidas, le espera un buen rato de entretenimiento. Al menos, el
que esto escribe no ha conseguido resolver la cuestión, ni encontrarla
resuelta. Lo malo es que tampoco acierta a demostrar que sea imposible.
|
| Autor: |
Mariano Nieto Viejobueno. |
| Publicado en: |
CARROLLIA-18, Septiembre de 1988 |
| Dificultad: |
*** |
| Solución: |
Pulse aquí |
 |
|
|
| Enunciado 042: Uno de aritmética.
|
|
Resolver la ecuación:
x.y.z
----- = k2
x+y+z
siendo x,y,z,k números
enteros
|
| Autor: |
Antonio Cebrián. |
| Publicado en: |
CARROLLIA-23 , Diciembre de 1989 |
| Dificultad: |
** |
| Solución: |
Pulse aquí |
 |
|
|
| Enunciado 043: La paradoja de Bertrand.
|
|
Esta paradoja surge
al tratar la solución al siguiente problema: Dada un circunferencia,
se traza en ella, al azar, una cuerda. ¿Cuál es la probabilidad
de que esta cuerda sea mayor que el lado del triángulo equilátero
inscrito en la circunferencia?
|
| Autor: |
Mariano Nieto Viejobueno. |
| Publicado en: |
CARROLIA-23. Diciembre de 1989 |
| Dificultad: |
*** |
| Solución: |
Pulse aquí |
 |
|
|
| Enunciado 044: Problema de los tres cuadrados. |
|
Propongo este problema
de geomtería que, a su vez, propone Martin Gardner en en
su libro Circo Matemático que, a su vez, se lo propuso
Lyber Katz que, a su vez, se lo propusieron en el colegio.
Gardner comenta que es de una sencillez fascinante y
Katz añade
que "el número de callejones sin salida a que conduce el problema
es extraordinario.
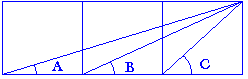
Tenemos tres cuadrados
iguale dispuestos como se muestra en la figura. Sirviéndose tan
sólo de geometría elemental (no es lícito usar trigonometría)
hay que demostrar que el ángulo C es igual a la suma de los
ángulos A y B.
|
| Autor: |
Propuesto por Aristogeronte. |
| Publicado
en: |
CARROLLIA-36. Marzo de 1993 |
| Dificultad: |
*** |
| Solución: |
Pulse aquí |
 |
|
|
| Enunciado 045: Un par de detectives astutos. |
|
Unos hábiles
detectives llegaron a la escena de lo que parecía ser un homicidio
y hallaron a la víctima tendida en un camino rural. La única
pista eran unas rodadas de neumático marcadas en el barro de la
poco transitada carretera. La pareja de detectives, muy astutos ellos,
siguió las rodadas hasta un caserío, distante alrededor de
un kilómetro. Había tres hombres sentados frente a la entrada,
y nada más verlos dedujeron quien era el sospechoso, aunque ninguno
tenía coche ni las botas manchadas de barro. ¿Cómo
pudieron resolver el caso tan rápidamente los detectives?
|
| Autor: |
Alejandro Ibrahim. |
| Publicado en: |
CIBERNETICA-4. Abril de 1987. |
| Dificultad: |
* |
| Solución: |
Pulse aquí |
 |
|
|