JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 041 a 045
Solución 041: Trasvases, un problema antiquísimo.
Por: Mariano Nieto
Hay un procedimiento gráfico para resolver este tipo de problemas que, normalmente, lleva a dos soluciones una corta y otra larga (con más trasvases).

Vamos a aplicarlo al caso 10, 7, 3. A la medida cuya capacidad es siete arrobas la llamaremos X y a la medida cuya capacidad es de tres arrobas Y. Trazamos dos ejes de coordenadas que formen un ángulo de 60 grados; sobre el eje de abscisas X llevaremos 7 divisiones y sobre el de ordenadas Y, 3. En el plano así definido podremos representar el estado de las dos medidas X, Y, mediante un punto cuyas coordenadas sean los respectivos contenidos. Cada trasvase estará representado por un vector cuyos origen y extremo estarán determinados por los contenidos de ambas medidas en sus estados inicial y final, es decir, antes y después de cada trasvase. Los sucesivos trasvases que resuelven el problema formarán una cadena de vectores que unen los puntos siguientes por este orden: (0,0), (7,0), (4,3), (4,0), (1,3), (1,0), (0,1), (7,1), (5,3) y (5,0). Obsérvese que los extremos de los vectores quedan siempre en el perímetro del paralelogramo definido por los vértices de coordenadas (0,0), (3,0), (7,3) y (0,7). El recorrido de los vectores se inicia en el origen de coordenadas, y se comporta igual que un rayo de luz que se fuese reflejando en los lados del paralelogramo como si estos fuesen espejos. Vemos, pues, que el problema se resulave con 9 trasvases. La segunda solución (que requiere diez trasvases) la obtendríamos mediante el recorrido (0,0), (0,3), ... Los números correspondientes a la cantidad a repartir y a las capacidades han de ser primos entre sí, de lo contrario, dividiendo por sus factores comunes, el problema quedaría reducido a otro análogo. Es evidente que la cantidad a repartir ha de ser siempre par. Siempre que la suma de las capacidades de las dos medidas sea igual a la cantidad a demediar, se observar que el número necesario de trasvases es igual al de la cantidad a repartir (solución larga); la solución corta tiene un trasvase menos. Por ejemplo, con los números 36,19 y 17 necesitamos 36 y 35 trasvases.

Si el Moya es el libro de matemática recreativa más antiguo en castellano, ¿ cuál podría considerarse el más antiguo del mundo ?. Ignoro la respuesta pero tal vez sea, al menos en Europa, la Aritmética de Beda el Venerable, sabio benedictino inglés que vivió a caballo de los siglos VII y VIII. En ella propone 55 problemas curiosos uno de los cuales es el conocidísimo del hombre, el lobo, la cabra y la col, problema que se ha ido transmitiendo de generación en generación hasta nuestros días.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 042: Uno de aritmética.
Por: Antonio Cebrián. 
Haciendo : 

x = a2(a+1); y=2a(a+1); z=a+1

x+y+z = (a2+2a+1) (a+1) = (a+1)3

x.y.z    a2(a+1).2a(a+1).(a+1)
------- = -------------------------------- = 2a3 = k2 ; haciendo a = 2n2; k = 4n3
x+y+z            (a+1)3 

x = 4n4(2n2+1) ; y = 4n2(2n2+1); z = 2n2+1
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 043: La paradoja de Bertrand.
Por: Mariano Nieto Viejobueno.
Solución 1: La posición de la cuerda puede ser determianda por su distancia al centro de la circunferencia. Esta distancia puede variar entre 0 y R. La cuerda será mayor que el lado del triángulo equilátero inscrito cuando su distancia al centro sea menor que R/2. De aquí obtenemos que la probabilidad buscada es 1/2.

Solución 2: Desde uno de los extremos de la cuerda trazamos la tangente a la circunferencia, el ángulo que forman las dos líneas, que varía entre 0o y 180o determina la posición de la cuerda. Para que la cuerda sea mayor que el lado del triángulo equilátero debe estar comprendida entre 60o y 120o. De ahí que la solución buscada sea 1/3.

Este resultado paradójico lo explica USPENSKY así:
 
    Estudiando atentamente ambas soluciones descubrimos que realmente estamos resolviendo dos problemas distintos. En la primera solución hemos supuesto que la distancia de la cuerda al centro tiene una distribución uniforme, mientras que, en la segunda, el ángulo es el que suponemos que tiene una distribución uniforme.
    La primera solución sería válida si la cuerda fuese la intersección de un disco con una de las líneas paralelas de un tablero rayado y distantes entre sí el disámetro del disco. La segunda solución respondería a una cuerda obtenida haciendo girar una tangente a la circunferencia alrededor del punto de tangencia, como si fuese un ruleta, al detenerse el movimiento quedaría definida la cuerda por la posición final.
     
Se puede aplicar a todos los problemas de esta clase la misma observación. Cuando cierto elemento geométrico, tal como un punto o una línea, se toma al azar, debería ser claramente indicado el macanismo de su obtención. Solamente entonces la supuesta distribución hipotética puede ser puesta a prueba experimental y confirmada (aproximadamente) o rechazada.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 044: Problema de los tres cuadrados.
Por: Aristogeronte.
Construcción que demuestra el teorema.


 
 
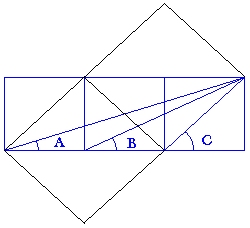Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 045: Un par de detectives astutos.
Por: Alejandro Ibrahim
No hay que suponer a priori que las rodadas eran de automóvil. Los detectives se habían dado cuenta de que las marcas habían sido producidas por una silla de ruedas y el sospechoso estaba sentado en una.
Ver Enunciado de este problema
(c) JGA, 1997 Los contenidos son de los autores, Mensa no sostiene ninguna idea Página principal