JUEGOS DE INGENIO DEL CLUB MENSA
(ENUNCIADOS 161 a 165) |
|
|
| Enunciado 161: La reina cruel y su astuto jardinero.
|
Hace muchos, muchos siglos atrás , una vieja reina
muy extravagante encargó a su jardinero que plantara
12 árboles en 6 filas de 4 árboles cada una,
de lo contrario haría cortar su cabeza. El jardinero
quedó asombrado por un instante, pero luego dijo que
lo haría con rapidez y facilidad.
¿Cómo
hizo el astuto jardinero para salvar su preciada vida?
|
| Autor: |
Propuesto por José Luis Hernández, de Argentina. |
| Publicado en: |
OMNIA. |
| Dificultad: |
* |
| Solución: |
Pulse aquí |
 |
|
|
| Enunciado 162: Un problema para obtusos.
|
Los astrónomos agrupan las estrellas, uniéndolas
por líneas imaginarias, en constelaciones. Tal vez, la
más sencilla sea la constelación formada por un
trío de estrellas. Consideremos la inmensa cantidad de
constelaciones triangulares que se formarían tomando las
estrellas del firmamento de tres en tres. Si las clasificásemos
en dos grupos, obtusángulas y acutángulas, ¿que
podríamos afirmar respecto a la abundancia de uno y otro?
El sentido común tal vez nos indique que debería
de haber más obtusángulas puesto que para ello basta
que sea obtuso uno cualquiera de los tres ángulos, pero
¿en qué proporción?
|
| Autor: |
Aristogeronte. |
| Publicado en: |
CARROLLIA-55. Diciembre de 1997. |
| Dificultad: |
** |
| Solución: |
Pulse aquí |
|
|
|
| Enunciado 163: El quinto postulado de Euclides.
|
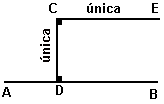 Tomemos
la recta AB y un punto C fuera de ésta. Vamos a demostrar que por
C puede trazarse una única paralela a AB, sin apoyarnos implícitamente
en la demostración, como solía ser el caso de tantos intentos
fallidos realizados a lo largo del tiempo.
Para ello nos apoyaremos
en un postulado anterior al quinto: siempre puede bajarse una única
perpendicular a una recta desde un punto cualquiera. Bajemos la perpendicular
CD desde el punto C a la recta AB. A dicha perpendicular levantamos a su
vez, en el punto C, la perpendicular CE. Esta última será
precisamente paralela a la recta AB en virtud del conocido teorema de las
dos perpendiculares a una recta (es legítimo citarlo puesto que
se demuestra antes del axioma del paralelismo).
Pero como antes se ha
dicho ambas perpendiculares son únicas. Luego la recta obtenida
CE es única.
(Nota
del editor: Las demostraciones de Perversus se caracterizan porque siempre
son falsas así que el avispado lector debe desenmascarar a este
siniestro personaje y descubrir el sofisma en el que ha basado su argumentación)
|
| Autor: |
Perversus. |
| Publicado en: |
CARROLLIA-55. Diciembre de 1997. |
| Dificultad: |
*** |
| Solución: |
Pulse aquí |
|
|
|
| Enunciado 164: El problema de las tres cajas. |
|
Es uno de los más
clásico en matemáticas recreativas. Tenemos tres cajas; en
una hay dos bolas blancas, en otra dos negras, en la tercera una blanca
y una negra. Sacamos a ciegas una bola de una de las cajas y resulta ser
blanca.
¿Cuál
es la probabilidad de que al sacar la otra bola de la misma caja ésta
sea también blanca?
|
| Autor: |
Anónimo. |
| Publicado
en: |
CARROLLIA-62. Septiembre de 1999. |
| Dificultad: |
** |
| Solución: |
Pulse aquí |
|
|
|
| Enunciado 165: Aficionados al teatro |
Miguel y Nadia fueron al teatro, cada
uno por su cuenta, pues no se conocían, a ver Hamlet, obra
que fue representada el año pasado en un teatro de la ciudad.
La obra fue interpretada durante veinte días en sesiones
de tarde y noche.
¿Qué posibilidades tenían de sentarse juntos,
uno al lado del otro, teniendo en cuenta que la platea del teatro
tiene 30 filas y en cada fila hay 28 asientos?
a) Suponemos que que la platea no está dividida por pasillo
alguno.
b) Suponemos que la
platea está dividida en dos, derecha e izquierda, números
pares e impares, por un pasillo central.
|
| Autor: |
Remitido por Miquel Clusa. |
| Publicado en: |
CARROLLIA-64. Marzo de 2000. |
| Dificultad: |
** |
| Solución: |
Pulse aquí |
|
|
|
