|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 161 a 165 |
| Solución
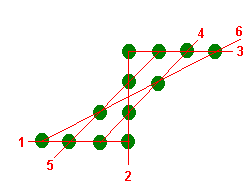
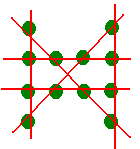
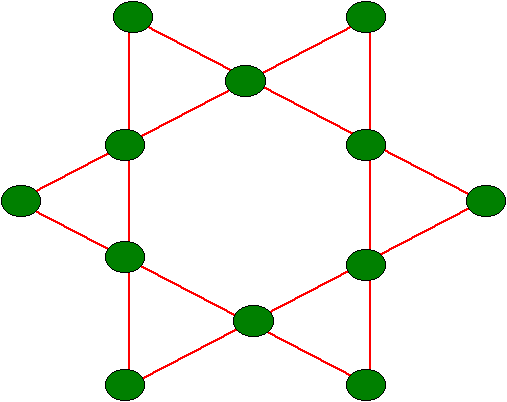
161: La reina cruel y su astuto jardinero. Por: Javier García Algarra. |
|
|
La siguiente disposición de los
árboles sobre el terreno cumple los caprichosos requisitos
de la reina:
Otra solución aportada por Diego Giannandrea:
|
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
162: Un problema para obtusos. Por: Aristogeronte |
|
La respuesta viene dada por la solución de este problema:
Dados tres puntos al azar ¿cuál es la probabilidad
de que el ángulo formado sea obtuso? 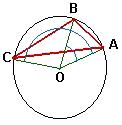 Sean A,
B y C los tres puntos. Hacemos pasar por ellos la
circunferencia de centro O. Para que el triángulo
ABC sea obtusángulo los tres puntos deberán
quedar del mismo lado de un diámetro. Para ello, si tomamos como referencia uno cualquiera de los tres puntos, por ejemplo el A, y medimos todos los ángulos en sentido antihorario, será necesario que los dos ángulos AOB y AOC sean menores de 180o, esto ocurrirá con una probabilidad 1/2 x 1/2 = 1/4; si esta condición se verifica para uno de los tres puntos, no se verifica evidentemente para los otros dos. Extendiendo el mismo razonamiento a los otros dos puntos, B y C, la probabilidad buscada es la suma de las probabilidades de cada punto, esto es 3/4. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
163: El quinto postulado de Euclides. Por: Perversus. |
|
En el razonamiento se comete el error llamado ignorantia elenchi
en lógica clásica, o sea, "incomprensión de
lo que se está demostrando". Efectivamente, mediante la construcción
citada obtenemos una única recta pero, ¿es que el
sistema de construcción de ésta es único? 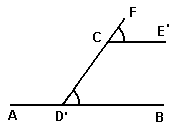 No. Existen
otros, por ejemplo el de la figura: en lugar de la base D de la
perpendicular CD podríamos tomar cualquier otro punto D'
en la recta AB, unirlo con C mediante la recta D'F y en el rayo
CF construir el ángulo FCE', igual al CD'B (y, además,
de modo que los rayos CE' y DB' se dispongan por el mismo lado de
FD'). En virtud del teorema (demostrado antes que el axioma) del
paralelismo de las rectas cuando son iguales los ángulos
correspondientes, podemes afirmar que la recta CE' es paralela a
la AB. Pero, ¿dónde está la garantía
de que las rectas CE' de las dos figuras contruidas coinciden? Afirmar
que diferentes contrucciones llevaran a la misma recta significa
tomar sin demostración aquello que tratábamos de demostrar.
|
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
164: El problema de las tres cajas. Por: Josep María Albaigès. |
|
|
A primera vista pudiera pensarse que ½,
pues de las dos cajas que contenían la bola blanca, una está
agotada y en la otra queda todavía otra blanca. Pero no es
así. Según el teorema de Bayes, la probabilidad de sacar bola blanca eligiendo una caja al azar era:   La probabilidad de obtener blanca en la segunda extracción, habiendo obtenido blanca en la primera, es obviamente la misma que la de haber elegido la primera caja, o sea:  Por tanto, la probabilidad pedida valdrá:  Si esta conclusión resulta chocante, piénsese en las distintas posibilidades de extracción: son para la primera bola BB, BB, BN,NB, NN, NN. Entre éstas, en tres sale blanca en primer lugar. Al sacar la segunda bola de entre ellas, en dos casos resulta ser también blanca. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
165: Aficionados al teatro Por: Josep María Albaigès. |
|
|
Llamaremos “asientos exteriores” a los
situados a los lados de la platea, e “interiores” a los restantes.
La probabilidad de que Miguel se siente en un asiento interior es
pi = 26/28, y la de exterior es pe = 2/28 Si Miguel está en un asiento interior, la probabilidad de que Nadia se siente en el mismo día y en la misma fila es 1/20×30 = 1/600. Si se da ese evento, la probabilidad de que se siente a su lado es 2/27. Análogamente, si está en uno exterior, la probabilidad de coincidencia, supuestas realizadas las de día y fila, se reduce a la mitad, 1/27. Por tanto, la probabilidad total es: p = 1/600 x [ (26/28 x 2/27) + (2/28 x 1/27)] = 1/8400 = 0,00119 8400 (Es más fácil el razonamiento: Para que Nadia pueda sentarse a la derecha de Miguel, éste deberá ocupar cualquier asiento excepto el extremo derecho, p = 27/28. Cumplida esta condición, la probabilidad de que Nadia se siente a su derecha es 1/(30×20×27) = 1/8100. Multiplicando ambas probabilidades y doblando para tener en cuenta el caso simétrico de Nadia a la izquierda, se obtiene el mismor esultado anterior).Efectuado este razonamiento, es fácil extenderlo al caso de varios pasillos. Si hay uno solo, es pi = 24/28; pe = 4/28, luego: p = 1/600 x [ (24/28 x 2/27) + (4/28 x 1/27)] = 13/11340 = 0,00115 |
|
| Ver Enunciado de este problema | |
|
||||||
