|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 011 a 015 |
| Solución
011: Un problema de huevos. Por: J. Alvarez Moure |
|
| Nadia aleccionó a sus hermanas para que vendieran los huevos por septenas, a 3 kopeks cada una, y cada huevo restante a 9 kopeks, con lo que cada una obtuvo exactamente 30 kopeks en total, cumpliendo las instrucciones de su madre. Parece que a sus compradores no les quedó otro remedio que aceptar su insólito sistema de venta, al no haber en el mercado más vendedoras de huevos. | |
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
012: Marchando una de Arquímedes. Por: Andrés García Parrilla |
|
| Cuando la moneda la tiene el pasajero, el volumen de agua que se desaloja por causa de la moneda es el necesario para igualar el peso de la moneda. Considerando que la densidad del agua es menor que la de la moneda, cuando la moneda cae al agua, se hunde, y por tanto el volumen de agua que desaloja es el mismo que el volumen de la moneda. La respuesta es que el agua bajará porque cuando la moneda está en poder del pasajero, el volumen desalojado de agua es superior al volumen de la moneda y cuando la moneda cae al agua el volumen de agua desalojada coincide con el de la moneda, luego en el segundo caso se desaloja menos agua y el nivel baja. | |
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
013: Juegos de manos, juegos de villanos. Por: Andrés García Parrilla. |
|
Llamando Na, Nb, Nc al número de
cartas que hay en los montones A, B y C respectivamente y P al punto
que hay que completar puede deducirse que:
|
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
014: Volare, oh, oh ! Por: Javier García Algarra. |
|
|
Es evidente que un avión sólo
no puede dar la vuelta al mundo. Dos, tampoco, pues resultaría
imposible que uno de ellos pudiese volver a la base, ya que la suma
de los dos depósitos sólo da para una vuelta. El número mínimo es tres. Llamemos L a la longitud de un círculo máximo. Cada avión dispone de combustible para L/2. Salen los tres aviones a la vez en el sentido de las agujas del reloj (es un suponer). Cuando han recorrido 1/8 de la esfera, los tres aviones disponen de 3L/8 de combustible cada uno. El avión A trasvasa L/8 al avión B y L/8 al avión C. Con ello, B y C tienen el depósito repleto y A suficiente para hacer el L/8 de vuelta a la base. Cuando B y C han recorrido otro L/8 (es decir, llevan un cuarto de planeta recorrido) sus depósitos contienen 3L/8. El avión B pasa a C L/8 y se queda con L/4 para volver a casa. Mientras tanto, el avión A ya ha vuelto a la base y lógicamente, C tiene el depósito lleno. Cuando C ha recorrido L/2 su depósito tiene todavía para recorrer L/4. En ese instante llega a la base el avión B y despega cargado hasta los topes en dirección contraria a las agujas del reloj. Cuando C ya está sin una gota de combustible porque ha recorrido 3L/4 aparece milagrosamente B y le cede L/8 del L/4 que le queda. Los dos aviones vuelan hacia la base que está a L/4 de distancia con combustible sólo para L/8, pero astutamente el avión A ha despegado en el mismo instante que B y C se encontraban. Cuando B y C están a 1/8 de círculo máximo de la base a punto de pegarse la chufa, llega A con sus 3L/8 de combustible y reparte L/8 a cada uno de los otros dos. Los tres vuelven a la base, habiendo completado C la vuelta al mundo. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
015: Equilibrio de mesas. Por: Miguel Angel Lerma |
|
|
Sean A, B, C y D los cuatro orificios
practicados sobre el tablero circular y O su centro. Para que la
mesa no guarde equilibrio los cuatro puntos deben quedar del mismo
lado de un diámetro. Esta condición se puede caracterizar
de la siguiente manera (los ángulos se miden siempre en sentido
antihorario de modo que adoptarán siempre cualquier magnitud
entre 0 y 360 grados): Para uno de los puntos, por ejemplo el A,
los ángulos AOB, AOC y AOD son menores que 180 grados. La
probabilidad de que cada uno de esos ángulos verifique la
condición es 1/2, y de que la verifiquen los tres es 1/8.
Como basta que esto suceda para uno de los puntos aún debemos
multiplicar esa cantidad por cuatro, es decir que queda 1/2. Este resultado puede generalizarse a n puntos, obteniéndose como probabilidad de equilibrio 1-(n/2(n-1)) . 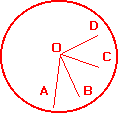 |
|
| Ver Enunciado de este problema | |
|
||||||