|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 016 a 020 |
| Solución
016: Los eslabones perdidos Por: Alejandro Ibrahim |
|
| La solución requiere abrir todos los eslabones de una de las cadenas (un total de 60 pesetas) y emplearlos en unir las otras tres (90 pesetas más). | |
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
017: Peligros de la intuición Por: Josep María Albaigès |
|
|
El problema es ilusorio. Basta con comparar
y se comprobará que el dado D gana también al A en
24 de cada 36 ocasiones. La asunción implícita de
que el concepto mejor que es transitivo debe descartarse.
Un análisis más a fondo demuestra que la simetría entre los dados dos a dos no se extiende al total. El dado A que, según hemos visto, gana al B y pierde con el D, empata con el C. El dado B, que pierde con el A y gana al C, pierde por poco con el D. Si se echaran simultáneamente los 4 dados, no ganarían todos por igual en las 1296 combinaciones posibles:
|
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
018: Problema geométrico. Por: Andrés García Parrilla |
|
|
Hay dos soluciones, según Carlos
esté más alejado o más próximo a Alicia.
Primera solución 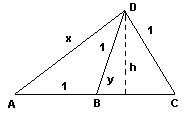 AB = 1; DB = 1; DC = 1; AD = AC = x; BH = y; DH = h AHD x² = (1+y)² + h² DHB 1 = y² + h² AD = AC x = 1 + 2y Resolviendo y = (-1+5½)/4 = 0.618 m (aprox)Segunda solución 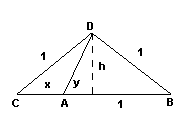 AHD x² = y² + h² DHC 1 = (x+y)² + h² DHB 1 = (1-y)² + h² Resolviendo x = (-1+5½)/2 = 1.618 m (aprox) |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
019: Las fracciones egipcias Por: Miguel Angel Lerma |
|
|
Sea r = p0 / q0 (p0 y q0 enteros) el número
racional elegido. Tomamos a0 como el mínimo entero positivo
tal que (1/a0)<=(p0/q0), y ponemos p1/q1 = p0/q0 -1/a0 = (p0a0-q0)/a0q0,
es decir, p1=p0a0-q0. En las siguientes etapas, se toma an como
el mínimo entero positivo no usado con anterioridad, tal
que 1/an<=pn/qn, y ponemos p(n+1) = pnan-qn, q(n+1)=anqn, de
modo que p(n+1)/q(n+1) = pn/qn - 1/an. Si en determinada etapa fuese p(n+1) = 0, el proceso terminaría y tendríamos que r = 1/a0 + 1/a1 + 1/a2 + ... + 1/an. Veremos que esto es precisamente lo que sucede, ya que la serie no puede proseguir indefinidamente. Cada denominador an (n>=1) es de una de estas dos clases: 1) an = a(n-1) + 1 , o bien 2) an > a(n-1) + 1, en cuyo caso an es el mínimo entero positivo tal que 0 <= pnan - qn. Esto implica que p(n+1) = pnan-qn < qn, pues de lo contrario sería 0 <= pn(an - 1 ) - qn y entonces an no sería mínimo. Si todos los denominadores fuesen de la primera clase, la serie no podría proseguir indefinidamente porque la serie armónica 1 + 1/2 + 1/3 + ... es divergente. Si algún denominador fuera de la segunda clase, entonces todos los que le siguen también lo son. En efecto: 1/(an - 1) > pn/qn = 1/an - p(n+1)/q(n+1) > 1/an + 1/a(n+1), luego 1/a(n+1) < 1/(an - 1) - 1/an, de donde a(n+1) > an(an -1) > = an + 1 . Puesto que esto implica que, a partir de ese punto será p(n+1)<pn, tampoco en este caso proseguirá la serie indefinidamente, o de otro modo, los pn constituirían una sucesión descendente ilimitada de enteros positivos. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
020: Solitario. Por: Andrés García Parrilla. |
|
| Un rey poderoso y rico con una serpiente al pie, un caballero con copa, y a su lado una mujer. Toma mujer esta copa, que yo con caballo y vara he de guardar el doblón porque este rey me lo manda. Al pie de un pino una fuente, un rey sediento llegó, a esta mujer pide ayuda y éste le ofrece un doblón. Un caballero valiente a esta mujer dio dinero y el rey por vengarse de ella le dio una copa de veneno. | |
| Ver Enunciado de este problema | |
|
||||||