|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 026 a 030 |
| Solución
026: Rompecabezas de colores. Por: Andrés García Parrilla. |
|
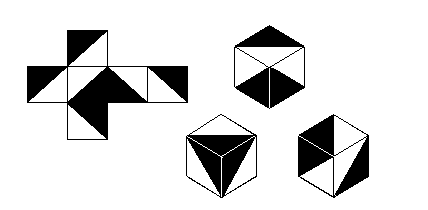
|
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
027: Triángulo Numérico. Por: Andrés García Parrilla. |
|
Llamaremos k a la suma de los números
de cada triángulo y para los nombres de las variables tomaremos
el siguiente convenio: 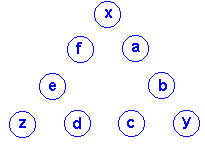 y + a + b = k z + c + d = k x + e + f = k y + z + a + b + c + d + e + f = 1 + 2 + 3 ... + 9 = 45Sumando las tres primeras y teniendo en cuenta la cuarta llegamos a que: k = (45 + x + y + z) / 3Este hecho es de gran ayuda pues nos permite deducir que todas las soluciones básicas verifican que la suma de x, y, z es un múltiplo de 3. Sólo hay 30 combinaciones de posibles valores de x, y, z, muchas de las cuales se pueden descartar fácilmente. k = 17 x y z a b c d e f ================= 1 2 3 5 9 4 8 6 7 1 2 3 6 8 5 7 4 9 k = 19 x y z a b c d e f ================= 1 4 7 5 9 2 6 3 8 1 4 7 6 8 3 5 2 9 2 3 7 5 9 1 8 4 6 2 3 7 6 8 4 5 1 9 k = 20 x y z a b c d e f ================= 1 5 9 6 8 2 4 3 7 2 5 8 4 9 1 6 3 7 2 5 8 6 7 3 4 1 9 3 5 7 4 8 2 6 1 9 4 5 6 2 9 1 8 3 7 4 5 6 3 8 2 7 1 9 k = 21 x y z a b c d e f ================= 3 6 9 4 8 1 5 2 7 3 6 9 5 7 2 4 1 8 3 7 8 2 9 1 5 4 6 3 7 8 5 6 2 4 1 9 k = 23 x y z a b c d e f ================= 7 8 9 2 6 1 5 3 4 7 8 9 3 5 2 4 1 6 |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
028: Ecuación de números enteros. Por: Andrés García Parrilla. |
|
|
No es ilógico pensar que habrá
algún tipo de regla general en la que particularizando podamos
llegar, simplemente dando los valores que queramos, a una solución.
Para buscar esta regla confeccionamos una lista de cuadrados y observamos que: 3² + 3² - 2 = 4² 3² + 4² = 5² 3² + 5² + 2 = 6² 3² + 6² + 4 = 7² 5² + 6² - 12 = 7² 5² + 7² - 10 = 8² 5² + 8² - 8 = 9² ... 5² + 13² + 2 = 14²Si tomamos el cuadrado de cualquier número impar, lo sumamos con el cuadrado de un segundo número y lo comparamos con el cuadrado del siguiente de este segundo se ve que la diferencia sigue una serie aritmética de razón dos y que sigue los números pares, luego pasará por el valor 2 que es el buscado. Además esto parece cumplirse para distintos primeros números impares, Apliquemos esta observación para la búsqueda de unos valores que resuelvan el problema. Imponemos la restricción de que z = x + 1 Sustituyendo y desarrollando (x+1)² = x² + 2x + 1 = x² + y² + 2 Para que sea cierta la igualdad debe cumplirse que 2x + 1 = y² + 2 Para cualquier valor de y mayor que 1 se ve que x > y. Por tanto y es el menor de los números. Podemos tomar pues y = 1992991, y despejando x = (y²+1)/2 = 1986006563041 z = x + 1 = 1986006563042 A otras soluciones podíamos haber llegado si en vez de hacer esta suposición hacemos otra pero la expresión para hallar x a partir de y no es tan sencilla. Siguiendo con esta línea de razonamientos podemos ver que se pueden conseguir tantos grupos de números como queramos que cumplan: x² + y² = z² y que además x + 1 = z Sustituyendo tenemos que x² + y² = x² + 2x + 1, de donde deducimos que x = (y²-1)/2, luego podemos elegir cualquier valor impar de y para obtener el x buscado. Ejemplo: y = 37 => x = 684 , z = 685 Si pensamos que estos números pueden ser las longitudes de los lados de un triángulo rectángulo es fácil deducir que podemos conseguir un triángulo tan estrecho como deseemos. Llamando w al ángulo formado por la hipotenusa y el cateto más largo tenemos que: w = arcotangente 2y/(y²-1) Está claro que el argumento del arcotangente decrece conforme aumenta el valor de y, luego también el ángulo decrece. Este hecho fue una de las claves que utilizó Miguel Angel Lerma para demostrar que el número de puntos que podemos situar en un plano, de forma que todas las distancias posibles entre ellos sean números enteros, es tan grande como deseemos. Para poder demostrar esto, situemos puntos alrededor de una circunferencia del siguiente modo: 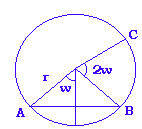 El triángulo formado por los vértices A, B y el centro de la circunferencia está formado por dos triángulos rectángulos iguales. Si elegimos los valores de todos los lados de manera que sean todos enteros, tendremos que todas las razones trigonométricas de w son racionales, también lo serán las de 2w, 4w ... El resto de distancias posibles, como la AC podrán obtenerse por trigonometría y serán forzosamente números racionales. Para que todas las distancias sean enteras basta hallar el mínimo común múltiplo de todos los denominadores y realizar el dibujo anterior a escala. Como podemos conseguir triángulos rectángulos de lados enteros tan estrechos como queramos, podemos situar en un plano un número tan grande de puntos como queramos de forma que las distancias entre ellos sean valores enteros. Miguel Angel Lerma también demostró que si vamos situando triángulos rectángulos aunque demos más de una vuelta los vértices nunca coinciden con los de vueltas anteriores. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
029: El mono de Lewis Carroll. Por: Josep María Albaigès. |
|
El problema no resiste el tratamiento
con métodos algo avanzados de Mecánica. El teorema
de las áreas barridas resulta de gran utilidad. 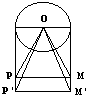 Si el mono pasa de M a M´(claro es que puede ascender, izándose a pulso como un gimnasta cualquiera), el peso P habrá pasado a una posición P'. Como no ha habido actuación de fuerzas exteriores al sistema, la suma algebraica de las áreas barridas desde el punto O (por donde pasa la resultante del sistema) será nula. O sea: Area OPP' = Area OMM'. Lo que es lo mismo PP'=MM'. El peso asciende a la misma velocidad del mono. Como este método de enfocar el problema tiene el inconveniente de decir muy poco a la imaginación, analicemoz el procedimiento con el que se iza el mono: contracción muscular del brazo-antebrazo. Esto provoca dos fuerzas de igual intensidad y sentio opuesto: la dirigida hacia arriba (aplicada en el hombro) izará al mono una altura dz, y la dirigida hacia abajo (aplicada en la mano) se transmitirá a trevés del hilo al peso, convertida en fuerza ascendente, con lo que elevará aquél en una cuantía igual a dz. No andaban descaminados quienes pronosticaban la inmovilidad del saco: imaginemos que los esfuerzos de izamiento del mono fueran muy pequeños y, consiguientemente, también las alturas dz. El tiempod de elevación, claro es, crecería. En el límite, la fuerza de izamiento sería nula: el peso no tendría medio alguno de "enterarse" de que al otro lado un mono intentaba ascender, puesto que no le llega ninguna fuerza a través del hilo: ¡el proceso de ascensión se ha convertido en lo que en Termodinámica se denomina una "transformación reversible"!. El mono ascendería sin que se moviera el saco de arena. Claro es que este ascenso tendría lugar en un tiempo infinito, lo que inhabilita esta abstracción el plano teórico. Pero, en la práctica, por pequeño que sea el rozamiento de la polea, siempre valdrá algo, y será posible elegir el esfuerzo de izamiento del mono lo suficientemente pequeño para ser absorbido por este rozamiento sin traducirse en una ascensión del peso P. Un paso al límite (rozamiento tendiendo a cero, fuerza tendiendo más aprisa a cero), nos reconduce a la misma situación. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
030: Un finlandés desdichado. Por: Javier García Algarra. |
|
|
Los extraterrestres eran unos sujetos
racionalistas que no podían imaginar la caprichosa forma
de medir la temperatura que tenía el finlandés. En
lugar de temperatura absoluta, el infeliz se expresaba en una extraña
escala basada en los puntos de fusión y ebullición
del agua. Así pues, para los extraterrestres, la exótica forma de vida tenía una temperatura de 310 Kelvin (37 grados centígrados), pero siguiendo su deseos la rebajaron a 155 Kelvin (118 grados centígrados bajo cero), causándole la muerte por congelación fulminante. |
|
| Ver Enunciado de este problema | |
|
||||||