|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 031 a 035 |
| Solución
031: ¿Cómo cortar el queso? Por: Josep María Albaigès. |
|
|
Para n=2 ó n=3 las soluciones con
triviales: el corte se hará según un diámetro
en el primer caso, y según tres sectores de 120 grados en
el segundo. Pero para n=4 la cosa comienza ya a complicarse. Pues un corte según cuatro sectores de noventa grados arrojaría una longitud de corte L=4, mientras que en el sistema indicado en la figura de la izquierda basta con L=3,9624. 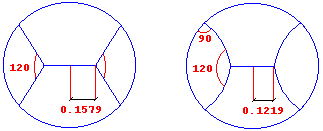 |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
032: ¿Discriminación? Por: Andrés García Parrilla. |
|
|
Ambas entidades pueden tener razón
porque más importantes que los promedios en sí mismos
son las cantidades que dieron origen a esos promedios. Para ilustrarlo,
lo mejor un ejemplo. En el departamento A se contrataron 4 de las
8 mujeres presentadas y 32 de los 80 hombres presentados. En el
departamento B se contrataron 10 de las 40 mujeres presentadas y
4 de los 20 hombres. Estos datos conducen a un 50% y un 40% de contratación para mujeres y hombres en el departamento A, y un 25% y un 20% respectivamente, para el departamento B. En conjunto, la empresa ha contratado a 14 de las 48 mujeres (29,1%) y a 36 de los 100 hombres con lo que vemos que ambas afirmaciones eran ciertas. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
033: Otra de naipes. Por: Andrés García Parrilla. |
|
|
Para explicarlo voy a suponer que sólo
tengo las 10 cartas de un palo. La solución es fácilmente
generalizable a cualquier número de cartas. Pensemos en que tenemos diez lugares en los que debemos ir colocando la carta adecuada. Es evidente que que los lugares primero, tercero, quinto, séptimo y noveno deberán estar ocupados por el As, 2, 3, 4 y 5. Una vez colocada la primera carta, el proceso que se ha seguido consiste en dejar un hueco y colocar la siguiente carta. Este es el proceso que deberemos aplicar hasta el final, pasar por alto un hueco y colocar la carta en el hueco siguiente. Por hueco entiendo cada uno de los lugares iniciales que aún están libres. Una vez colocado el 5 en el noveno lugar dejamos pasar el hueco décimo y ponemos el 6 en el siguiente hueco que es el segundo. Dejamos pasar el cuarto y colocamos el 7 en el sexto. Saltamos el octavo y ponemos la sota en el décimo y finalmente ponemos en rey en el cuarto. Las cartas de arriba a abajo, quedarían colocadas del siguiente modo: As, 6, 2, Rey, 3, 7, 4, Caballo, 5, Sota. Este procedimiento es extrapolable a cualquier número de cartas y generalizable para cualquier relación cartas vueltas/ cartas puestas. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
034: Uno de cinemática. Por: Josep María Albaigès. |
|
|
Para este problema se han recibido soluciones
basadas en álgebra, pero resultan algo largas. Puede ser
una buena ocasión para recordar el teorema de las esferas
isocronas, tan útil en casos como éste, y que
parece algo olvidado. Como es fácil comprobar, un móvil
partiendo mediante un plano inclinado del polo N de una esfera alcanza
cualquier punto de ésta en el mismo tiempo t = 2(R/g)½.
En el caso precedente, las dos esferas centradas en Oa y Ob deberán tener el mismo radio. La condición de tiempo mínimo exige que sean tangentes, así que dicho radio será la mitad de la distancia AB, igual, por paralelismo, a la OaOb. 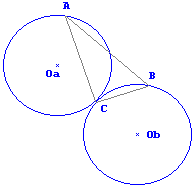 |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
035: Ecuación diofántica Por: Antonio Cebrián Gil. |
|
Haciendo: x = 3a ; y = 3b ; z =3c ; t = 3dresulta que: 33a + 35b + 37c = 38dSi hacemos: 3a = 5b = 7c; 3.3^a = 3^8d; 3a + 1 = 8d 5b + 1 = 8d 7c + 1 = 8dSe tiene que cumplir que 3.5.7.m + 1 = 8d Resolviendo esta última ecuación resulta que m = 7, d = 92. De aquí que a = 5.7.7. = 245; b = 3.7.7 = 147; z = 3.5.7 = 105Una solución sería: x = 3245 ; y = 3147 ; z = 3105 ; t = 392 |
|
| Ver Enunciado de este problema | |
|
||||||