|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 036 a 040 |
| Solución
036: El timo del empeño. Por: Desconocido miembro de MATH SIG |
|
|
Nadie tuvo la crueldad de explicarle que
el billete le había costado seis dólares (incluyendo
los tres del desempeño). [Nota del editor: He visto muchos problemas tontorrones, pero éste se llevaría seguro el segundo premio en el campeonato del mundo de problemas bobos]. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
037: La ruleta rusa. Por: Otro miembro anónimo de MATH SIG. |
|
En la ruleta rusa habitual su probabilidad
de muerte es 1/6 = 0,167. Con el artificio propuesto, la probabilidad
de que el revólver no haya disparado todavía a la
n-sima vez es:
p1 = (5/6)nEl sexto jugador sucumbirá si el revólver se dispara la vez sexta, duodécima, etc. Es decir: p = (1/6)[(5/6)5 + (5/6)11 + ...] = 55/(66-56) = 0,101[Nota del editor: Mejor no hacer el experimento] |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
038: El harén del sultán. Por: Desconocido socio de British Mensa. |
|
|
Tras el decreto, un cincuenta por ciento
de los primogénitos serán varones (e hijos únicos),
y un cincuenta por ciento, hembras, muchas de las cuales tendrán
hermanos menores. Dentro de este segundo grupo, habrá un
cincuenta por ciento de segundones que serán varones (y con
ellos se acaba la familia), y un cinuenta por ciento de hembras.
En ese otro subconjunto se reiterará la proporción.
Es decir, que la población del país constará de una serie de subconjuntos (el de los primogénitos, el de los segundones, el de los tercerones...), todos ellos equilibrados. ¡La proporción 50%-50% se mantendrá!. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
039: Sólo para artilleros. Por: Andrés García Parrilla. |
|
|
Trazamos la perpendicular OH a la recta
s y tomamos esa distancia sobre la perpendicular OA a t' y obtenemos
el punto B. Por B trazamos una recta s' perpendicular a OB. Si llamamos
R al alcance del cañón, las cuerdas de las rectas
s y s' dentro de la circunferencia de radio R y centro O son iguales.
Antes de continuar, fijémonos en que los puntos D, E, I, J definen un trapecio en el que DI=L1 y EJ=L2. Sea C el punto medio de AB, si trazamos la perpendicular a OA por el punto C obtenemos los puntos F y G. La distancia FG es igual a L'=(L1+L2)/2=L/2, y además, como los lados del trapecio DE e IJ son cuerdas de la circunferencia, las perpendiculares a éstas por sus puntos medios F y G pasan por el centro O de la circunferencia. Ahora ya estamos en condiciones de poder determinar el radio, tenemos las rectas s', t y los puntos A y B, hallamos C, punto medio de AB y trazamos por C la perpendicular de longitud L/2 que nos fija los puntos Fy G. Los unimos con el punto O y trazamos las perpendiculares a estas rectas, y determinamos los puntos D, E, I, J. La distancia de cualquiera de estos puntos al punto O es el radio de la circunferencia. 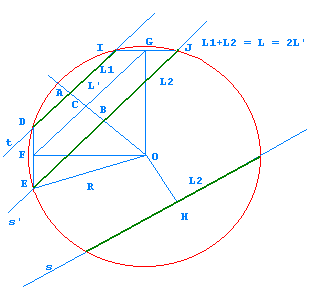 |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
040: Torneo de tenis. Por: Andrés García Parrilla. |
|
|
SOLUCIÓN INTUITIVA El número de posibles emparejamientos es Cn,2. En un partido cualquiera de una ronda cualquiera deberá jugar una pareja, la probabilidad de que esta pareja sea la que nos interesa es 1/Cn,2. El número de partidos que se juegan en el torneo es n-1, ya que en cada partido un jugador es eliminado y al final sólo queda el ganador. La pareja que nos interesa podrá encontrarse en cualquiera de esos partidos, luego la probabilidad pedida es (n-1)/Cn,2 = 2/n. SOLUCIÓN FORMAL Supongamos que la solución es pn=2/n y procedamos por inducción. Llamamos A y B a los jugadores que componen la pareja. Para el caso de n=2 es trivial que se cumple. Supongamos que se cumple hasta n y veamos que esto implica que se cumple para n+1. Distinguimos el caso de que n+1 sea par o impar. Si n+1 es par todos los participantes juegan en la ronda inicial. El jugador A puede quedar emparejado con n rivales. La probabilidad de que el rival de A sea B es 1/n. En el caso de que no se enfrenten en la primera ronda, la probabilidad de que los dos pasen a la segunda ronda es 1/4 y el número de jugadores que quedan es (n+1)/2; la probabilidad de que se encuentren a partir de aquí es p(n+1)/2 = 2/[(n+1)/2]=4/(n+1). Obtenemos que pn+1 = 1/n + (n-1)/n * 1/4 * 4/(n+1) = 2/(n+1). Si n+1 es impar hay un jugador que libra en la primera ronda. La probabilidad de que A ó B libren es 2/(n+1), en este caso la probabilidad de que el otro pase a la segunda ronda es de 1/2, el número de jugadores para la segunda ronda es 1+n/2, y la probabilidad de que se encuentren a partir de ahí es p(n+2)/2 = 4/(n+2). La probabilidad de que ni A ni B libren en la primera ronda es (n-1)/(n+1). A puede quedar emparejado con n-1 rivales (todos los demás menos el que libre). La probabilidad de que este rival sea B es 1/(n-1). La probabilidad de que ese rival no sea B es (n-2)/(n-1). Es este caso la probabilidad de que ambos pasen a la segunda ronda es 1/4 y quedarán para esa ronda 1+n/2 jugadores. Obtenemos que: pn+1=2/(n+1) * 1/2 * 4/(n+2) + (n-1)/(n+1) * [1/(n-1) + (n-2)/(n-1) * 1/4 * 4/(n+2)] =2/(n+1) |
|
| Ver Enunciado de este problema | |
|
||||||