|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 076 a 080 |
| Solución
076: Calcular el radio de la Tierra. Por: Josep María Albaigès |
|
Partamos antes de unas fórmulas
bien conocidas de los estudiantes. La distancia marítima
a que puede alcanzarse con la vista desde una altura h es calculable
fácilmente: 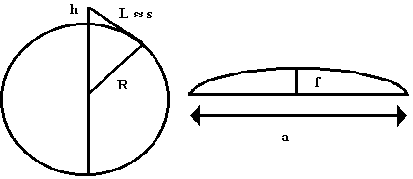 Si desde el punto V, tierra adentro y por encima del nivel del mar, miramos éste superponiéndolo visualmente a la barandilla del paseo marítimo (o de la terraza del apartamento), las visuales hasta los extremos del mar visible formarán un ángulo horizontal q . La distancia entre los extremos del horizonte visible, a la que llamaremos a, vale: 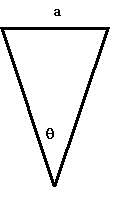 Utilizando ahora (3), resulta: 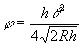 Por ejemplo, sea: q = 0,20 j = 0,00002 |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
077: La ecuación biografía de Diofanto. Por: Josep María Albaigès |
|
|
Con los medios algebraicos actuales, el
planteamiento de la ecuación es inmediato. Si era x su edad
al morir, entonces: x/6 + x/12 + x/7 + 5 + x/2 + 4 = x
Cuya inmediata solución es 84. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
078: El guardarropa. Por: Aristogeronte |
|||||||||||||||||
|
Consideremos todas las permutaciones de los elementos a1, a2 ... an (cuyo número, como es sabido es n!) y llamemos a una de ellas permutación base. Dada otra permutación de los mismos n elementos, llamaremos fijos a aquellos elementos que coincidan en posición con los de la base. Por último, llamaremos permutaciones completas (pc) a aquellas que no contengan elementos fijos. En el problema del guardarropa, una pc corresponderá a un caso en que nadie recibe su propio sombrero. Sea wn el número total de pc de n elementos. Es fácil ver que w1= 0, w2 = 1, w3 = 2, ... Demostremos ahora la igualdad : wn = (n-1)wn-1 + (n-1)wn-2[1] El primer sumando de la expresión [1] corresponde al número de pc de n elementos, que pueden obtenerse partiendo de cada una de las pc de (n-1) elementos, por el proceso de sustiyuir uno de sus (n-1) elementos ai por el nuevo an, colocando el ai como nuevo elemento de la pc. Supongamos ahora una cualquiera de las pc de orden n; si intercambiamos de posición el elemento an y el último, podrá ocurrir que éste, en la nueva permutación obtenida, se convierta en fijo, lo que quiere decir que la pc de la que partíamos no fue originada por el proceso anterior sino por el otro , partiendo de un apermutación de orden (n-1) con un sólo lemento fijo éste se sustituye por an y el fijo se coloca al final. El número de permutaciones de orden (n-1) con un sólo elemento fijo es precisamenre (n-1)wn-2, que corresponde al segundo sumando de la fórmula [1], con lo que esta queda justificada. Llamemos pn a la probabilidad de que un apermutación de orden n sea completa. pn = wn/n! p1 = 0, p2 = 1/2 De [1] deducimos que vn = -(n-1)/n pn-1 + 1/n pn-2, n(pn - pn-1) = -(pn-1 - pn-2) Haciendo pn - pn-1 = vn tendremos que nvn = -vn-1. Se ve que vn = 1/n! con signo + ó - según la paridad de n. Finalmente llegamos a pn = 1/2! + 1/3! + ... + 1/n! que tiende al número 1/e cuendo n aumenta, es decir cuando crece el número de sombreros. El valor aproximado de 1/e es 0,367879 . En la tabla podemos ver la correspondencia entre el número de sombreros y la probabilidad de que nadie reciba el suyo, y cómo se estabiliza rápidamente hacia el valor 1/e.
|
|||||||||||||||||
| Ver Enunciado de este problema | |||||||||||||||||
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |||||||||||||||||
| Solución
079: Ecuación diofántica kilométrica. Por: Josep María Albaigès. |
|
| Los números pedidos son simplemente los cocientes de las sucesivas divisiones enteras del número 506878 por 7, es decir, 1, 3, 5, 7, 0, 2 y 4. Los coeficientes son simplemente las potencias de 7, así que las incógnitas son la expresión del número dado expresado en esa base. | |
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
080: El castillo encantado. Por: Mariano Nieto |
|||||||||||||||||||||||||||||||
|
Las condiciones pueden resumirse así:
A - SI NO(RISA) Y ORGANO -> CANTO CAMBIA B - En cualquier otro caso CANTO NO CAMBIA C - SI INCIENSO -> RISA hará lo contrario que canto D - SI NO(INCIENSO), la risa hará lo mismo que el canto
Al quemar incienso en el minuto 1, en el 2 la risa no se oirá (por C). En el minuto 2, el canto se oirá, tanto si el órgano suena como sin no (por A y B). Al quemar incienso en el minuto 2, en el 3 la risa no se oirá (por C). Al sonar el órgano en el minuto 2, en el 3 el canto no se oirá (por A). Al no quemar incienso en el minuto 3, en el 4 la risa no se oirá (por D). Al no tocar el órgano en el minuto 3, en el 4 el canto no se oirá (por B). Por consiguiente, las manipulaciones que haremos serán: en el primer minuto quemar incienso; en le segundo minuto quemar incienso y tocar el órgano, a partir del tercer minuto dejaremos de tocar el órgano y quemar incienso y la calma será eterna ... |
|||||||||||||||||||||||||||||||
| Ver Enunciado de este problema | |||||||||||||||||||||||||||||||
|
||||||