|
JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 141 a 145 |
| Solución
141: Siete primos equidistantes. Por: Josep María Albaigès |
|
|
La primera condición permitiría
buscar entre números pequeños, pero la segunda nos
indica que la solución debe ser un número alto. En realidad, la búsqueda llevó 52 días de trabajo a un conjunto de siete ordenadores de alta velocidad trabajando con técnicas especiales de investigación de números primos y según procedimientos matemáticos especiales (resolución de ecuaciones modulares). El primer paso consistió en computar m, el producto de los 48 primeros primos: m = 367009731827331916465034565 550136732339800312955331782619 462457039988073311157667212930 A continuación hubo que hallar la solución de 48 ecuaciones modulares, de la que resultó: x = 118930613432425504731600916 625360539894173228870159415462 976014056809082107560202605690 Seguidamente hubo que buscar entre la sucesión Pi = x + Nm + 1, esperando que aparecieran 7 primos consecutivos en ella. El primer éxito se dio para: N= 2968677222 De donde resultó el primer primo de la sucesión: P1 = 1089533431247 0593108757803789229577329080 3649299313819538521310556174 2150447308967213141717486151 Los restantes, claro, son P2 = P1 + 210; P3 = P2 + 210;… P7 = P6 + 210. ¡Una muestra más de matemáticas inútiles, pero bellas! |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
142: El dado casquivano. Por: Josep María Albaigès |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Supongamos que la aparición del primer
6 no debe producirse hasta el lanzamiento n+1, y calculemos ante
todo el número de "casos posibles" es decir, el número
de posibles lanzamientos del dado. Éste corresponderá
claramente al número de variaciones con repetición
totales que pueden producirse con 6 elementos tomados n a n. Dicho
valor será Y pasemos ahora a la determinación de los "casos favorables". Éstos formarán parte del subconjunto de permutaciones con repetición de n elementos en las que no aparece ningún 6, o sea obviamente Pero de éstas habrá que descontar aquéllas en que no aparezca ningún 1, ningún 2, etc., pues todos los números deben aparecer al menos una vez. El número 1 no aparece en Pero de éstas habrá que descontar las contadas dos veces, o sea aquéllas en que no aparece ningún 1 ni ningún 2, o ningún 1 ni ningún 3, etc. En total, Y ahora hay que descontar de este descuento las permutaciones, ya contadas, en que no aparece ningún 1 ni ningún 2 ni ningún 3, o ningún 1, ningún 2 ni ningún 4, etc. En total, Y así sucesivamente. Es decir, que en total el número de permutaciones será:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ver Enunciado de este problema | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Solución
143: Números ordenados en la Lotería Primitiva. Por: Josep María Albaigès. |
|
|
El número de combinaciones distintas
de números premiados es ciertamente importante: Dada una cualquiera de ellas, los seis números que la integran podrán haber salido de 6! = 720 maneras diferentes. Y sólo una de ellas guarda el orden ascendente de números, por tanto la probabilidad pedida es: 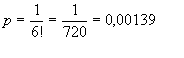
Es decir, que solamente en un 0,13 % de los sorteos saldrán los números por orden. En toda la historia de la lotería primitiva desde que se reinstauró apenas habrá sucedido esto una vez. En general, para n números, la probabilidad sería 1/n!. |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
144: Dígitos repetidos en la sucesión de potencias de 2. Por: Josep María Albaigès. |
|
|
Según las pistas, la parte decimal
de n log 2 está uniformemente distribuida en el intervalo
(0,1), y por tanto sus antilogaritmos (las potencias de 2) lo estarán
de forma logarítmica, conque la primera cifra se repartirá
en el intervalo (0,10) de la misma forma, en logaritmo decimal.
Es decir: Cifras que empiezan con 1: 30,10 % (log 2) 2: 17,61 % (log 3 - log 2) 3: 12,49 % (log 4 - log 3) etc. El problema está emparentado con el de la distribución aleatoria de la primera cifra de un número cualquiera, sea la producción anual de acero en USA o la magnitud bolométrica de una estrella. Desde antiguo se había observado que las páginas de las tablas de logaritmos están más usadas en los números bajos que en los altos. La segunda parte sigue de inmediato. El bloque 10298 tendrá una frecuencia de aparición proporcional a log (10299/10298), o sea 0,00422 %. Miguel Ángel, dando el resultado por bueno, añadió algunas precisiones: Es verdad, aunque los detalles son algo más complejos. En una primera aproximación podríamos tomar un intervalo [1,N] y calcular la probabilidad de que un número elegido al azar (con probabilidad uniforme) en dicho intervalo empiece por determinada cifra. Luego computamos el límite de dicha probabilidad cuando N tiende a infinito. Desgraciadamente dicho límite no existe, aunque sí existen un «límite inferior» y un «límite superior» (diferentes). Por ejemplo, si miramos a los números que empiezan por 1, entre 1 y 9 hay 1, por tanto su proporción hasta ahí es 1/9 = 0,11111111..., pero entonces encontramos los números 10, 11,..., 19, que empiezan por 1, así que la proporción sube hasta 11/19 = 0,5789473684... para N=19, y a partir de ahí baja hasta 11/99 = 0,11111111... para N=99, luego sube hasta 111/199 = 0,5577889447... para N=199, y así sucesivamente. La proporción de números que empiezan por 1 va oscilando pues entre una serie de máximos y mínimos que convergen respectivamente a un límite superior (5/9 = 0,55555555... en este caso) y a un límite inferior (1/9 = 0,11111111...) diferentes. En casos como éste a veces es preferible calcular el límite en sentido Césaro, es decir, en vez de lim a(N) calculamos lim (a(1) +... + a(N))/N. Esta técnica, por ejemplo, permite asignar «límite» a sucesiones oscilantes como 1, 0, 1, 0,... (que en sentido Césaro tiene límite 1/2). Sin embargo en el problema que nos ocupa el límite en sentido Césaro tampoco existe, aunque los límites superior e inferior obtenidos se hallan más próximos. El paso al límite en sentido Césaro se puede reiterar indefinidamente: a(0,N) = a(N) a(1,N) = (a(0,1) + ... + a(0,N))/N a(2,N) = (a(1,1) + ... + a(1,N))/N Y así sucesivamente. En este problema tras infinitas reiteraciones los límites inferior y superior acaban coincidiendo, con lo cual es posible hablar del «límite» de la probabilidad de que un número natural elegido «al azar» comience por una cifra dada c. Si no recuerdo mal dicha probabilidad es precisamente el logaritmo decimal de (c+1)/c. Una pregunta que uno se podría hacer es, si 10298 puede considerarse como una «cifra» en base 100000, ¿por qué calculamos la frecuencia correspondiente con un logaritmo decimal en vez de un logaritmo en base 100000? |
|
| Ver Enunciado de este problema | |
| Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. | |
| Solución
145: El Nim Por: Josep María Albaigès y Miguel Angel Lerma |
|
|
1. Supongo que cada jugador puede escoger
el montón que quiera. Entonces un jugador puede acabar con
las fichas del primer montón, pues éste nunca puede
ser repuesto. Después del primero vendrá el segundo
(que ahora ha pasado a ser primero) y así sucesivamente.
La prueba se basa en que el primer montón de la izquierda
sólo puede disminuir. Si sólo hubiera un montón,
entonces es obvio que terminaría por acabarse. En el
caso general procedemos por inducción. Supongamos que el
juego con n montones necesariamente acaba. Bajo esa hipótesis
probaremos que con n+1 montones también tiene que terminar.
En efecto, si los jugadores nunca tocaran el primer montón
entonces estarían jugando sólo con los n montones
restantes, los cuales por hipótesis acabarían por
terminarse. Por lo tanto tarde o temprano alguno de los jugadores tendrá que tomar alguna ficha del primer montón. Esta consideración se puede repetir mientras queden fichas en el primer montón, el cual seguirá disminuyendo hasta agotarse. Tras ello quedarán a lo más n montones, lo cual nos dejaría otra vez en la situación supuesta en la hipótesis de inducción. 2. La estrategia se parece mucho a la del juego de retirar entre una y tres piedras de un solo montón. Basta con hacer que en cada montón haya un múltiplo de 4, retirando las fichas, en el montón a suprimir, de forma que se mantenga esa cifra. Puesto que el contrario no puede tomar más de 3 fichas del montón elegido, tras su movimiento habrá estropeado la pauta, pero el primer jugador podrá dejar otra vez un múltiplo de 4 tomando las fichas necesarias del mismo montón y añadiendo las que sean necesarias en los montones que hay a la derecha de éste para que también en ellos haya siempre un múltiplo de 4. 3. Se tratará de hacer que haya un número par de montones, vigilando la multiplicidad en el último, y además deben ser iguales por parejas de montones consecutivos. Por ejemplo, una configuración favorable para el jugador que acaba de jugar sería: 5, 5, 12, 12, 7, 7. Aclaró posteriormente M. Á.: En cuanto a las posibilidades de prolongar el juego por un tiempo arbitrariamente largo, aún es posible, pero ahora sólo si los dos jugadores colaboran para ello. Sin embargo, si quedan al menos cuatro montones y uno de los jugadores esta usando la estrategia ganadora, entonces el que está perdiendo puede hacer que el juego dure tanto como quiera: le basta con poner muchas fichas en un par de montones consecutivos y luego ir retirándolas una a una. |
|
| Ver Enunciado de este problema | |
|
||||||