JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 151 a 155
Solución 151: La oferta enológica.
Por: Josep María Albaigès.
El máximo valor del descuento se obtendrá cuando el promedio se aleje lo más posible de la
botella más próxima a él. Cuando las seis botellas son del mismo valor, el descuento es d = 1/6 = 16,67%.

Si compramos tres botellas de un precio p1 y otras tres de un precio mayor p2, la media es obviamente (p1+p2)/2. La distancia de este valor tanto a la barata como a la cara es (p2-p1)/2. En este caso podría plantearse la duda de si la botella de obsequio es la barata o la cara, pero es fácil soslayar esta dificultad sustituyendo una de las botellas caras por una de un precio ligeramente inferior.
En definitiva, si los precios son (p1,p1,p1,p2, p2, p2-e), el valor promedio es ahora: Este valor está ligeramente más cerca de p2 que de p1, conque la botella regalo será la última de
que hemos hablado, y el descuento es por tanto: 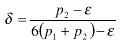Este valor tiene como límite superior: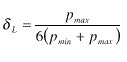 
Por ejemplo: si el precio mínimo es 500 Pta/botella y el máximo 1000 Pta/botella, la estrategia a seguir consistiría en comprar 3 botellas de a 500, 2 de a 1000 y una de a 999. Con ello el descuento se aproximaría a su límite superior, dL= 1000/4500 = 22,22 %.
El máximo absoluto se alcanzaría si hubiera botellas de valor nulo. Sería dLmax= 1/3 = 33,33 %,
fuera cual fuera el valor de las botellas caras adquiridas.
Similarmente podemos proceder para hallar el límite inferior del descuento: se tratará de que una
de las botellas quede lo más lejos posible del valor medio, esta vez por defecto. La estrategia es simétricaa la anterior: comprarlas de valores (p1-e, p1, p1, p2, p2, p2), con lo que el valor promedio es ahora: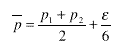

El límite inferior será 1/6 = 16,67 %.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 152: Una curiosa propiedad cuadrática.
Por: Josep María Albaigès

Si existe una ley, la correspondiente ecuación tomará la forma:

Desarrollando y simplificando se llega a:

O sea, finalmente:

n = 2p(p + 1)

De donde salen fácilmente los siguientes términos:

36 2 + 37 2 + 38 2 + 39 2 + 40 2 = 41 2 + 42 2 + 43 2 + 44 2
55 2 + 56 2 + 57 2 + 58 2 + 59 2 + 60 2 = 61 2 + 62 2 + 63 2 + 64 2 + 65 2

Obsérvese que la base del último cuadrado del término de la izquierda es siempre el
cuádruple de un número triangular.

Estas series presentan una analogía trivial con las del tipo:

1 + 2 = 3
4 + 5 + 6 = 7 + 8
9 + 10 + 11 + 12 = 13 + 14 + 15

que es también muy fácil generalizar.

Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 153: Signo matemático perdido.
Por: Anónimo.
El punto decimal, para obtener 1.2 .
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 154: El solitario de la abuela.
Por: Josep María Albaigès.
Si la baraja tuviera únicamente un palo, el problema sería muy fácil: se trataría de que la permutación de las cartas fuera absoluta, es decir, que el número de orden la ninguna carta nunca coincidiera con su propio número. Según las leyes de la combinatoria, la probabilidad de que esto ocurra es, para n cartas:



Pero para barajas de dos o más palos la cosa se vuelva bastante más complicada. Pues en estos casos hay que evaluar las probabilidades de coincidencias en un lugar, en dos, en tres, etc., lo que genera expresiones algebraicas enormemente tediosas.

Por suerte, podemos resolver el problema más rápidamente aprovechando la rápida convergencia de la expresión anterior. Para un número muy grande de cartas, la probabilidad de no coincidencia de una carta en un lugar es  , por lo que, para los n lugares, será . El solitario saldrá una de cada tres veces aproximadamente.

Fácilmente se concluye que cuando el número de palos es k, la expresión pasa a ser:



Para el caso propuesto por Roberto, el valor sería p = e-4 = 0,0183. Es decir, un 1,8 % de las veces. Ciertamente es un solitario difícil, pero asequible.

Para afinar un poco más en el resultado, puede utilizarse el método de Monte-Carlo, "jugando" mediante el ordenador el solitario repetidas veces. Las probabilidades que se obtienen son bastante parecidas a las calculadas. Para la baraja de 12 cartas, sale tras 10.000 ensayos de cada solitario:
 
 
p
e-k
 p
e-k
 p
e-k
 p
e-k
 p
e-k
 p
e-k
n
4
8
12
16
20
24
k
1
0.370 
0.368 
0.370 
0.368 
0.366 
0.368 
0.364 
0.368 
0.367 
0.368 
0.368 
0.368 
2
0.117 
0.135 
0.128 
0.135 
0.128 
0.135 
0.130 
0.135 
0.131 
0.135 
0.129 
0.135 
3
0.037 
0.050 
0.045 
0.050 
0.048 
0.050 
0.047 
0.050 
0.052 
0.050 
0.043 
0.050 
4
0.010 
0.018 
0.014 
0.018 
0.015 
0.018 
0.016 
0.018 
0.017 
0.018 
0.017 
0.018 
5
0.003 
0.007 
0.005 
0.007 
0.006 
0.007 
0.006 
0.007 
0.007 
0.007 
0.005 
0.007 
6
0.002 
0.002 
0.002 
0.002 
0.003 
0.002 
0.002 
0.002 
0.002 
0.002 
0.002 
0.002 
7
0.001 
0.001 
0.001 
0.001 
0.001 
0.001 
0.001 
0.001 
0.001 
0.001 
0.001 
0.001 
8
0.000 
0.000 
0.000 
0.000 
0.000 
0.000 
0.000 
0.000 
0.000 
0.000 
0.000 
0.000 


Como puede verse, los valores reales tienden rápidamente hacia los calculados. Para el caso concreto de Roberto, tras 100.000 ensayos se obtiene p = 1,53 %, valor algo inferior al previsto con la fórmula aproximada.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 155: Jugando con la calculadora
Por: Anónimo.
Valor máximo:

3/ 7 + 5 x 4 - 3 = 18.71

Valor mínimo:

3 / 7 - 5 x 4 + 3 = -15.29
Ver Enunciado de este problema
(c) JGA, 2000 Los contenidos son de los autores, Mensa no sostiene ninguna idea Página principal