JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 186 a 190
Solución 186:
Por: A. Trujillo

Nota: La solución que apareció originalmente en CARROLLIA-67 era incorrecta. Dos lectores de la edición electrónica, Agustín Trujillo y Pablo Sussi repararon en el error y han proporcionado la solución correcta.

Solución de Agustín Trujillo:

Hojeando el problema de Alex y David no estoy de acuerdo con la solución que propones. Yo obtengo otra diferente.

A ---------(2/3)---------- x ----(1/3)----- D

Alex (A) recorrerá el doble de distancia que David (D), ya que corre el doble de rápido. En
realidad, A habrá hecho (cuando se crucen) los 2/3 del trayecto, y D sólo 1/3. Por el reloj de D habrán transcurrido 31 minutos en hacer 1/3 de la distancia que separa sus casas.
Veamos ahora la segunda situación

A ---(1/3)----- x ----(2/3)---- D1(12:10) ---(1/9)--- D0(12:00)

D sale de su casa (D0). A los 10 minutos, (mientras A está aún parado), D habrá hecho 1/9 de
la distancia (ya que antes tardó 30 min. en hacer 1/3). Quedan aún 8/9 entre ellos cuando A sale.
Como A corre a la mitad de velocidad que D, D hará los 2/3 de la distancia que falta (8/9 del total) y A hará el 1/3 restante. Es decir, que cuando se crucen, D habrá recorrido 1/9+2/3*8/9 = 19/27 del trayecto.
Teniendo en cuenta que por el reloj de D transcurren 31 min. en hacer 1/3 del camino, por regla
de tres obtenemos que en hacer 19/27 se tardaría (por el reloj de D) 19*31/9 = 65.4444 min. Es decir,
que por el reloj de D sería la una y cinco de la tarde (y 26 segundos) cuando se cruce con A.

Solución de Pablo Sussi:

Si David recorre en 30 minutos, la mitad de lo de Alex, entonces se encuentran en el punto en el que Alex recorrió 2/3 y David 1/3.
Quiere decir que David recorre en 30 minutos 1/3 del camino, por lo tanto por minuto recorre 1/90 del camino.Como Alex el segundo día va a mitad de velocidad, irá entonces a 1/180.
Llamamos t al tiempo que tarda David el segundo día:
1/90*t+1/180*(t-10)=1
1/60*t=1+1/18
t=60*19/18=190/3= 63.333333 minutos
Como su reloj adelanta al ritmo de 31/30, habrán pasado 63.3333*31/30=65.44444 minutos de las 12
o sea marcará 13 horas 5 minutos 26.66 segundos
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 187:
Por: Josep María Albaigès
Me advertía un profesor de Matemáticas en mis años mozos que “la intuición es fuente constante de error”.
Y a error nos conduciría la fácil conclusión de que la sucesión responde a la fórmula un= 2n-1 .
Pues en efecto, al elegir un sexto punto, ¡el término resultante es 31! El número de regiones definidas por n puntos responde a la fórmula:

Al avanzar en la sucesión, ésta diverge cada vez más de los valores intuidos, como se ve en el cuadro: n E(n) 2 n-1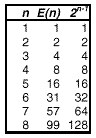

Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 188:
Por: Josep María Albaigès
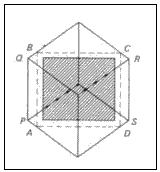Sí es posible. Si observamos el cubo “de punta” (esto es, con la visual en la dirección de la diagonal principal; para mayor claridad, se ha dibujado un poco desviada) veremos la figura adjunta, que es un hexágono regular cuyo lado es el del cubo. Dado el rectángulo punteado, BC puede ser tan próximo como queramos a la diagonal de una cara, y AB será siempre mayor que el lado. Por tanto, en su interior cabe un cuadrado de lado igual al del cubo. Perforando éste según el cuadrado, otro cubo pasará perfectamente por el orificio.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 189:
Por: Javier García Algarra
La única dificultad de este problema radica en el enunciado, que más parece un trabalenguas. Si llamamos ep y ej a las edades de Pepe y Juan, respectivamente, podemos escribir que:
ej+ ep = 91 [i].
En un momento del pasado, sabemos que la edad de Pepe era la misma que la que tiene Juan ahora. Si eso sucedió hace n años, podemos escribir que:
ep - n = ej [ii]
También sabemos que la edad actual de Pepe es el doble de la que tenía Juan en ese momento del pasado (hace n años).
Por tanto: ep = 2 (ej - n) [iii]
Despejando las ecuaciones [ii] y [iii] averiguamos que ej = 3n, y despejando con este resultado [i] y [ii] descubrimos
que ej = 39 y ep = 52.
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 190:
Por: Javier García Algarra
La serie está compuesta de un número secuencial (1, 2, 3 ...) seguido de un número primo empezando por 2 (2, 3, 5, 7, ...)

El siguiente número secuencial es el 11 y el siguiente primo, el 31. En consecuencia el término que sigue la serie es 1131.
Ver Enunciado de este problema
(c) JGA, 2001 Los contenidos son de los autores, Mensa no sostiene ninguna idea Página principal